Hình bên dưới minh họa một cái lều hai mái là hai hình chữ nhật giống nhau trong không gian $Oxyz$

Hình bên dưới minh họa một cái lều hai mái là hai hình chữ nhật giống nhau trong không gian $Oxyz$. Biết các kích thước của mái lều là $SA=5m$, $AB=10m$, độ cao từ $S$ xuống mặt đất là $4m$. Bạn An muốn trang trí chiếc lều bằng cách treo các sợi dây cờ trang trí từ các góc lều $O,A,B,C$ đến đuôi một chiếc đèn treo từ vị trí chính giữa của $SQ$, cách $SQ$ $19cm$. Hỏi tổng chiều dài sợi dây cờ trang trí tối thiểu bạn An cần mua là bao nhiêu mét? (kết quả làm tròn đến hàng phần mười)

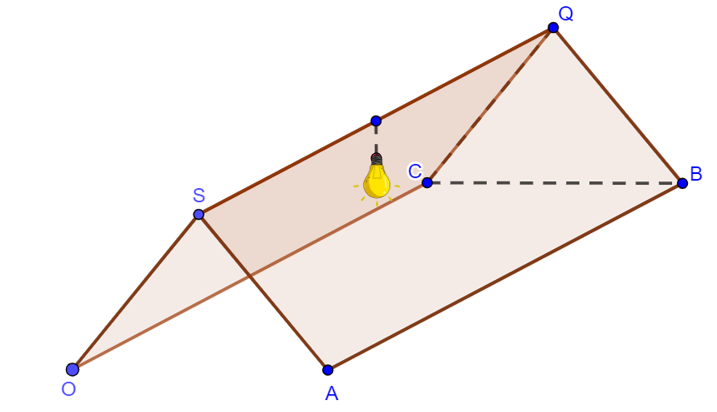
Đáp án: 27,9
Lời giải:

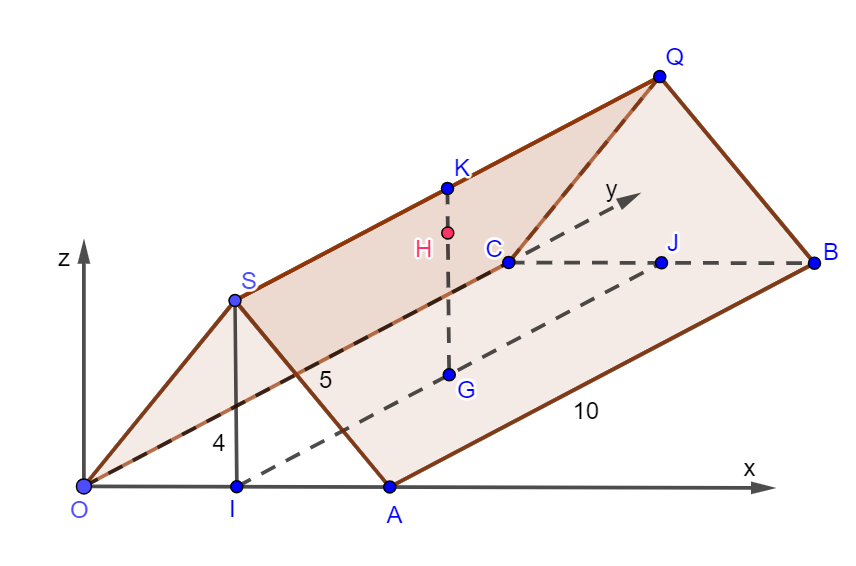
Gắn hệ trục tọa độ $Oxyz$ như hình vẽ. Gọi $I,K$ lần lượt là trung điểm của $OA,SQ$. $OA=2IA=2\sqrt{{{5}^{2}}-{{4}^{2}}}=6$ Gọi $H$ là vị trí chiếc đèn, $KH=19cm=0,190m$. Gọi $G$ là giao điểm của hai đường chéo của hình chữ nhật $OABC$, suy ra $HG=4-0,190=3,810m$. Do đó $H\left( 3;5;3,810 \right)$. Ta thấy: $OH=AH=CH=BH$ nên tổng chiều dài sợi dây màu xanh tối thiểu bạn An cần mua là $4OH$ Ta có: $\overrightarrow{OH}=\left( 3;5;3,810 \right)\Rightarrow 4OH=4.\sqrt{{{3}^{2}}+{{5}^{2}}+{{\left(3,810 \right)}^{2}}}\approx 27,86140\left( m \right)$