Một chiếc cổng hình Parabol có chiều cao $9\,m$, khoảng cách giữa hai chân cổng là $6\,m$

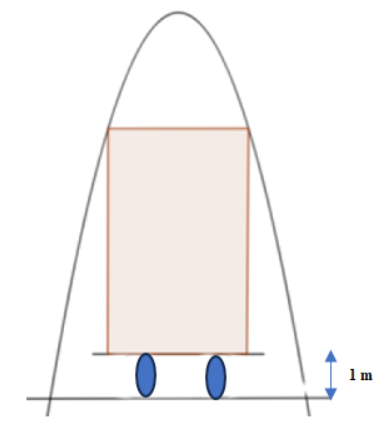
Một chiếc cổng hình Parabol có chiều cao $9\,m$, khoảng cách giữa hai chân cổng là $6\,m$. Để vận chuyển thùng hàng hình chữ nhật qua cổng, người ta dùng một xe kéo có chiều cao $1\,m$. Biết rằng mặt cắt của thùng hàng qua cổng là hình chữ nhật, hỏi diện tích hình chữ nhật đó lớn nhất là bao nhiêu$\,{{m}^{2}}$để xe chở thùng hàng có thể đi qua được cổng (kết quả làm tròn đến hàng phần chục).

Lời giải

Đáp án: $17,4$.

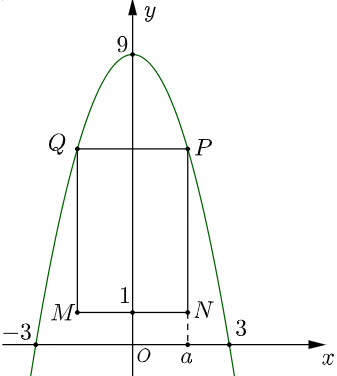
Trong hệ trục toạ độ $Oxy$ như hình vẽ, chiếc cổng hình parabol có phương trình $y=-{{x}^{2}}+9$Xe chở hàng có thể đi qua được cổng nếu điểm $P$ thuộc parabol với hoành độ điểm $P$ bằng $a,\,\,a\in \left( 0;\,3 \right)$. Khi đó tung độ của điểm $P$ bằng $-{{a}^{2}}+9$ và $\left\{ \begin{align}

& MN=2a \\

& NP=-{{a}^{2}}+9-1=-{{a}^{2}}+8 \\

\end{align} \right.$

Diện tích của hình chữ nhật là $S=MN.NP=2a.\left( -{{a}^{2}}+8 \right)=-2{{a}^{3}}+16a$

Ta có: ${S}’=-6{{a}^{2}}+16=0\Leftrightarrow a=\pm \frac{2\sqrt{6}}{3}$. Do$\,\,a\in \left( 0;\,3 \right)$ nên $a=\frac{2\sqrt{6}}{3}$.

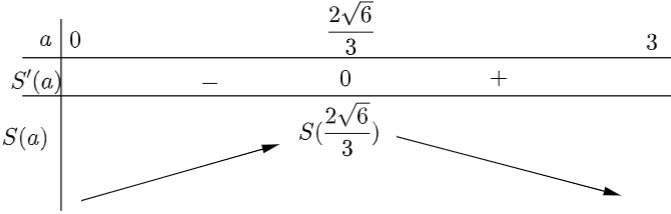
Khi đó ${{S}_{\max }}=S\left( \frac{2\sqrt{6}}{3} \right)\simeq 17,4\,\left( {{m}^{2}} \right)$.