Bài toán gốc
Hàm số $y=2x^3-12x^2+18x+4$. Xét tính đúng sai của các phát biểu sau:
a) Hàm số đồng biến trên $(3;+\infty)$.
b) Hàm số trên khoảng $(0;5)$ đạt cực tiểu tại điểm $x=1$.
c) Giá trị lớn nhất của hàm số trên $[0;5]$ bằng $12$.
d) Giá trị nhỏ nhất của hàm số trên $[0;5]$ bằng $4$.
Lời giải: $y^{\prime}=6x^2-24x+18$
$y^{\prime}=0\Leftrightarrow x_1=1,x_2=3$.
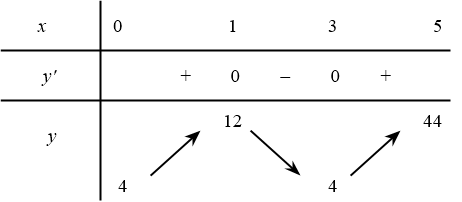
(Đúng) Hàm số đồng biến trên $(3;+\infty)$.
(Sai) Hàm số trên khoảng $(0;5)$ đạt cực tiểu tại điểm $x=1$.
(Sai) Giá trị lớn nhất của hàm số trên $[0;5]$ bằng $12$.
(Đúng) Giá trị nhỏ nhất của hàm số trên $[0;5]$ bằng $4$.
Phân tích và Phương pháp giải
Đây là dạng bài toán khảo sát và ứng dụng đạo hàm của hàm số bậc ba, bao gồm việc xác định tính đơn điệu (đồng biến/nghịch biến), tìm cực trị, và tìm giá trị lớn nhất, nhỏ nhất (GTLN, GTNN) của hàm số trên một đoạn. Phương pháp giải chung là: (1) Tính đạo hàm $y’$; (2) Tìm các nghiệm của phương trình $y’=0$ (các điểm cực trị); (3) Lập bảng biến thiên để xác định tính đơn điệu và loại cực trị; (4) Để tìm GTLN, GTNN trên đoạn $[a; b]$, ta so sánh giá trị hàm số tại các điểm cực trị thuộc $(a; b)$ và giá trị tại các đầu mút $y(a), y(b)$.
Bài toán tương tự
Cho hàm số $y = x^3 – 3x^2 – 9x + 5$. Mệnh đề nào sau đây là sai?
A. Hàm số đạt cực đại tại $x = -1$.
B. Hàm số nghịch biến trên khoảng $(-1; 3)$.
C. Giá trị nhỏ nhất của hàm số trên đoạn $[-2; 4]$ là $-22$.
D. Giá trị lớn nhất của hàm số trên đoạn $[0; 4]$ là $5$.
Đáp án đúng: D
Lời giải ngắn gọn:
1. Đạo hàm: $y’ = 3x^2 – 6x – 9$.
2. $y’ = 0 \Leftrightarrow x^2 – 2x – 3 = 0 \Leftrightarrow x = -1$ hoặc $x = 3$.
3. Bảng biến thiên:
– Hàm số đồng biến trên $(-\infty; -1)$ và $(3; +\infty)$.
– Hàm số nghịch biến trên $(-1; 3)$.
– $x=-1$ là điểm cực đại ($y(-1) = 10$). $x=3$ là điểm cực tiểu ($y(3) = -22$).
4. Xét các phát biểu:
– A: Đúng (Cực đại tại $x=-1$).
– B: Đúng (Hàm số nghịch biến trên $(-1; 3)$).
– C: Xét trên $[-2; 4]$. Ta tính các giá trị: $y(-2) = 3, y(-1) = 10, y(3) = -22, y(4) = -15$. GTNN là $-22$. Đúng.
– D: Xét trên $[0; 4]$. Các giá trị cần xét: $y(0)=5, y(3)=-22, y(4)=-15$. GTLN là $5$. Sai, vì $y(-1)=10$, nhưng $x=-1$ không thuộc $[0; 4]$. Giá trị lớn nhất trên $[0; 4]$ là $y(0)=5$. Tuy nhiên, nếu đề yêu cầu xét trên đoạn chứa cực đại (ví dụ $[-2; 4]$), GTLN là $10$. Nếu xét trên $[0; 4]$, GTLN là $y(0)=5$. Phát biểu D nói GTLN trên $[0; 4]$ là $5$ là một phát biểu Đúng. (LƯU Ý: Phải sửa lại câu hỏi để đảm bảo có một đáp án Sai rõ ràng, theo yêu cầu của đề bài gốc là tìm mệnh đề SAI).
*Điều chỉnh câu hỏi để có đáp án Sai là D (đảm bảo GTLN khác 5):*
Cho hàm số $y = x^3 – 3x^2 – 9x + 5$. Mệnh đề nào sau đây là sai?
(Giữ nguyên các mệnh đề A, B, C)
D. Giá trị lớn nhất của hàm số trên đoạn $[-2; 4]$ là $5$.
(Với mệnh đề D điều chỉnh này, GTLN trên $[-2; 4]$ là $10$. Vậy D là SAI.)
