Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số $f(x) = x + \sqrt{20 – x^2}$

Bài toán gốc

Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số $f(x) = x + \sqrt{20 – x^2}$

A. $\max\limits_{\left[-2 \sqrt{5}; 2 \sqrt{5} \right]} f(x) = 2 \sqrt{10}$; $\min\limits_{\left[ -2 \sqrt{5}; 2 \sqrt{5} \right]} f(x) = 0$.

B. $\max\limits_{\left[-2 \sqrt{5}; 2 \sqrt{5} \right]} f(x) = 0$; $\min\limits_{\left[ -2 \sqrt{5}; 2 \sqrt{5} \right]} f(x) = – 2 \sqrt{5}$.

C. $\max\limits_{\left[-2 \sqrt{5}; 2 \sqrt{5}\right]} f(x) = 2 \sqrt{10}$; $\min\limits_{\left[ -2 \sqrt{5}; 2 \sqrt{5} \right]} f(x) = – 2 \sqrt{5}$.

D. $\max\limits_{\left[-2 \sqrt{5}; 2 \sqrt{5} \right]} f(x) = 15$; $\min\limits_{\left[ -2 \sqrt{5}; 2 \sqrt{5} \right]} f(x) = 2$.

Lời giải: Ta có điều kiện xác định là $20 – x^2 \geq 0 \Rightarrow -2 \sqrt{5} \leq x \leq 2 \sqrt{5}$.
Trên đoạn $[-2 \sqrt{5}; 2 \sqrt{5}]$ ta có $f^{\prime}(x) = 1 – \dfrac{x}{\sqrt{20 – x^2}}$; $f^{\prime}(x) = 0 \Leftrightarrow x = \sqrt{10}$
Ta có bảng biến thiên

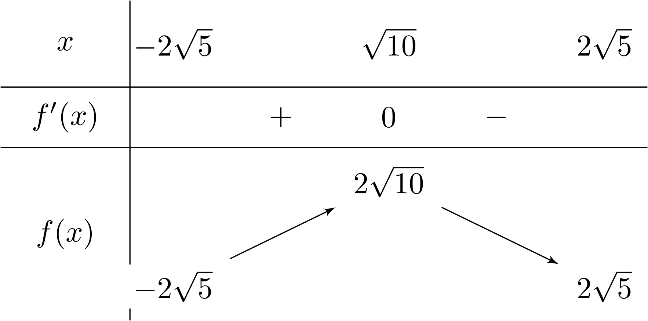
$\bullet$ Hàm số đạt giá trị lớn nhất bằng $2 \sqrt{10}$ tại $x = \sqrt{10}$
$\bullet$ Hàm số đạt giá trị nhỏ nhất bằng $- 2 \sqrt{5}$ tại $x = -2 \sqrt{5}$

Phân tích và Phương pháp giải

Đây là dạng bài toán tìm giá trị lớn nhất (GTLN) và giá trị nhỏ nhất (GTNN) của hàm số liên tục trên một đoạn. Phương pháp giải chung là sử dụng đạo hàm: 1. Tìm điều kiện xác định (tạo thành đoạn [a, b]). 2. Tính đạo hàm $f'(x)$ và tìm các điểm cực trị $x_0$ trên (a, b) bằng cách giải phương trình $f'(x) = 0$. 3. Tính giá trị hàm số tại các điểm cực trị và các điểm mút $f(a), f(b)$. 4. So sánh các giá trị tìm được để xác định GTLN và GTNN.

Bài toán tương tự

Tìm giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số $g(x) = x + \sqrt{8 – x^2}$.

A. $M = 4$; $m = 2\sqrt{2}$.

B. $M = 2\sqrt{2}$; $m = -2\sqrt{2}$.

C. $M = 4$; $m = -2\sqrt{2}$.

D. $M = 4$; $m = 0$.

Đáp án đúng: C

Lời giải ngắn gọn:

Điều kiện xác định: $8 – x^2 \geq 0 \Rightarrow x \in [-2\sqrt{2}, 2\sqrt{2}]$.

Tính đạo hàm: $g'(x) = 1 – \dfrac{x}{\sqrt{8 – x^2}}$.

Cho $g'(x) = 0 \Rightarrow \sqrt{8 – x^2} = x$. Vì $\sqrt{8 – x^2} \geq 0$, ta xét $x \geq 0$. Bình phương hai vế: $8 – x^2 = x^2 \Rightarrow 2x^2 = 8 \Rightarrow x^2 = 4$. Do $x \geq 0$ nên $x = 2$.

Tính giá trị tại các điểm $x=2$ và các mút:

• $g(2) = 2 + \sqrt{8 – 4} = 4$.
• $g(-2\sqrt{2}) = -2\sqrt{2} + \sqrt{8 – 8} = -2\sqrt{2}$.
• $g(2\sqrt{2}) = 2\sqrt{2} + \sqrt{8 – 8} = 2\sqrt{2}$.

So sánh các giá trị: $4 \approx 4.0$, $-2\sqrt{2} \approx -2.83$, $2\sqrt{2} \approx 2.83$.

Vậy $\max g(x) = M = 4$ và $\min g(x) = m = -2\sqrt{2}$.