Một đường dây điện được nối từ một nhà máy điện ở A đến một hòn đảo ở

C. Khoảng cách ngắn nhất từ C đến B là 2 km. Khoảng cách từ B đến A là 9 km.

Bài toán gốc

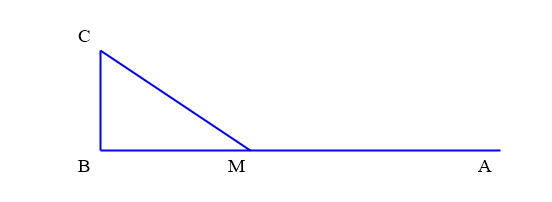
Một đường dây điện được nối từ một nhà máy điện ở A đến một hòn đảo ở

C. Khoảng cách ngắn nhất từ C đến B là 2 km. Khoảng cách từ B đến A là 9 km. Mỗi km dây điện đặt dưới nước mất 5000 USD, còn đặt dưới đất mất 4000 US

D. Hỏi chi phí thấp nhất là bao nhiêu ngàn USD?

A. $42$.

B. $39$.

C. $40$.

D. $45$.

Lời giải: Đặt $AM=x$, hàm số chi phí là $f(x)=4000x+5000\sqrt{2^2+(9-x)^2}$, $x\in (0;9)$. Chi phí thấp nhất khi $x=\dfrac{19}{3}$.

Phân tích và Phương pháp giải

Đây là dạng toán tối ưu hóa (tìm giá trị nhỏ nhất) ứng dụng trong thực tế, cụ thể là tìm chi phí thấp nhất để lắp đặt đường dây điện. Phương pháp giải là sử dụng đạo hàm để khảo sát hàm chi phí. Thiết lập hàm chi phí $C(x)$ phụ thuộc vào khoảng cách lắp đặt trên đất liền ($x$), sau đó tìm điểm cực tiểu của hàm số bằng cách giải phương trình đạo hàm $C'(x)=0$. Hàm chi phí có dạng $C(x) = C_{dat} imes x + C_{nuoc} imes ext{khoảng cách dưới nước}.

Bài toán tương tự

Một công ty muốn kéo đường cáp quang từ nhà máy A đến khu du lịch C nằm trên một hòn đảo. Khoảng cách ngắn nhất từ C đến bờ sông tại B là 3 km. Khoảng cách dọc bờ sông từ B đến A là 12 km. Chi phí lắp đặt mỗi km cáp dưới đất là 3000 USD, và mỗi km cáp dưới nước là 5000 USD. Hỏi chi phí thấp nhất để lắp đặt đường cáp quang là bao nhiêu ngàn USD?
A. 50
B. 48
C. 46
D. 45

Đáp án đúng: B. 48
Lời giải ngắn gọn:
Gọi M là điểm đặt cáp trên đoạn AB sao cho AM = x (km), với $x \in [0; 12]$.
Đoạn cáp trên đất liền là AM = x (chi phí $3x$ ngàn USD).
Đoạn cáp dưới nước là MC. Ta có MB = $12 – x$. MC = $\sqrt{BC^2 + MB^2} = \sqrt{3^2 + (12-x)^2}$.
Hàm chi phí (ngàn USD): $C(x) = 3x + 5\sqrt{9 + (12-x)^2}$.
Lấy đạo hàm và cho $C'(x) = 0$: $3 – \frac{5(12-x)}{\sqrt{9 + (12-x)^2}} = 0$.
Giải phương trình, ta tìm được $(12-x)^2 = 81/16$, suy ra $12-x = 9/4$. Do đó $x = 12 – 9/4 = 39/4$.
Khi $x = 39/4$, chi phí thấp nhất là $C(39/4) = 3(39/4) + 5(15/4) = (117 + 75)/4 = 192/4 = 48$ (ngàn USD).