Đề: Tìm tất cả các giá trị của m để phương trình \(- {x^3} + 3{x^2} + m = 0\) có 3 nghiệm thực phân biệt. 

Xét hàm số \(y = f\left( x \right) = – {x^3} + 3{x^2} + m\)

Gọi A, B là 2 điểm cực trị của đồ thị hàm số

\(f’\left( x \right) = – 3{x^2} + 6x \Rightarrow f’\left( x \right) = 0 \Leftrightarrow x = 0;x = 2\)

\(\Rightarrow A\left( {0,m} \right);B\left( {2,m + 4} \right)\)

Do hệ số của \(x^3\) âm nên A là điểm cực tiểu và B là điểm cực đại.

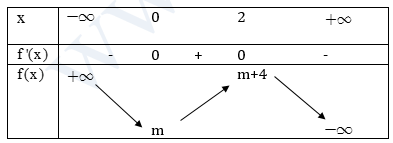
Do phương trình \(- {x^3} + 3{x^2} + m = 0\) có 3 nghiệm phân biệt nên A, B phải nằm về 2 phía của trục hoành nên \(m

\(\Rightarrow – 4