Sự tương giao của đồ thị

Sự tương giao của đồ thị – Sự tương giao của đường cong…

Ví dụ 1.  Cho hàm số $y=x^3-3x$.
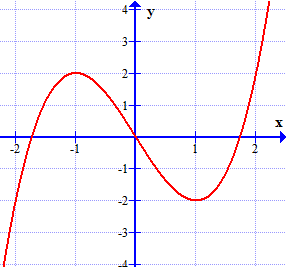
a) Khảo sát sự biến thiên và vẽ đồ thị $\left ( C \right )$ của hàm số.
b) Dựa vào đồ thị $\left ( C \right )$ hãy biện luận theo tham số $m$ số nghiệm của phương trình: $x^3-x=m^3-3m \ \ \ \ (2.1)$.
Giải
a)Đồ thị:
Số nghiệm của phương trình $(2.1)$ bằng số giao điểm của đồ thị $\left ( C \right )$ và đường thẳng $y=m^3-m$. Ta có các trường hợp sau:
* TH1: $\left [ \begin{matrix}m^3-m2 \end{matrix}\right.\Leftrightarrow \left [ \begin{matrix}m < -2\\m > 2 \end{matrix}\right.$ Khi đó phương trình $(2.1)$ có đúng 1 nghiệm duy nhất.*TH2: $\left [ \begin{matrix}m^3-3m=-2\\m^3-3m=2 \end{matrix}\right.\Leftrightarrow \left [ \begin{matrix}m=\pm 2\\m = \pm 1 \end{matrix}\right.$. Khi đó phương trình $(2.1)$ có 2 nghiệm phân biệt

*TH3: $-2<m^3-m<2 \Leftrightarrow \left\{\begin{matrix}-2<m<2\\m\neq \pm 1\end{matrix}\right.$. Khi đó phương trình $(2.1)$ có đúng 3 nghiệm phân biệt

Ví dụ 2.  Cho hàm số $y=x^3+3x^2-4$.
a) Khảo sát sự biến thiên và vẽ đồ thị $\left ( C \right )$ của hàm số.
b) Dựa vào đồ thị $\left ( C \right )$ hãy biện luận theo tham số $m$ số nghiệm của phương trình: $\left |x^3+3x^2-4 \right |=m \ \ \ \ (2.2)$.
Giải
a) Đồ thị:

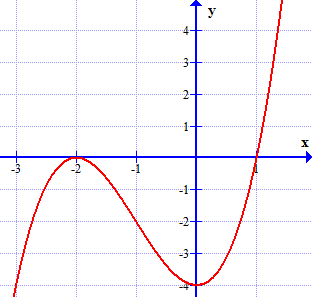
b) Đặt $f(x)=x^3+3x^2-4$. Ta có:
$$g(x)=\left |x^3+3x^2-4 \right | = \left | f(x) \right | = \left\{\begin{matrix} f(x)&\textrm{khi } f(x) \geq 0\\ -f(x)&\textrm{khi } f(x) < 0\end{matrix}\right.$$
Như vậy, muốn vẽ đồ thị hàm số $y=g(x)$, ta làm như sau:
– Giữ nguyên phần phía trên trục $Ox$ của đồ thị $\left ( C \right )$,
– Lấy đối xứng phần phía dưới $Ox$ của $\left ( C \right )$ qua $Ox$
– Xóa phần phần phía dưới $Ox$ của $\left ( C \right )$.
Ta có đồ thị hàm số $y=g(x)$ là đường màu xanh trong hình sau:

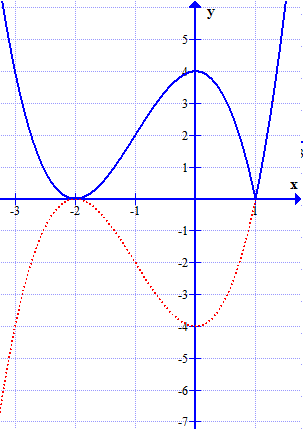
Số nghiệm của phương trình $(2.2)$ bằng số giao điểm của đồ thị hàm số $y=g(x)$ và đường thẳng $y=m$. Ta có các trường hợp sau:
* TH1:Nếu $m<0$ thì phương trình $(2.2)$ vô nghiệm
*TH2: Nếu $m=0$ hoặc $m>4$ thì phương trình $(2.2)$ có đúng 2 nghiệm phân biệt
*TH3: Nếu $0<m<4$ thì phương trình $(2.2)$ có đúng 4 nghiệm phân biệt
*TH4: Nếu $m=4$ thì phương trình $(2.2)$ có đúng 3 nghiệm.

Ví dụ 3.  Cho hàm số $y=\frac{x-2}{x+1}$
a) Khảo sát sự biến thiên và vẽ đồ thị $\left ( C \right )$ của hàm số.
b) Dựa vào đồ thị $\left ( C \right )$ hãy biện luận theo tham số $m$ số nghiệm của phương trình: $\frac{|x-2|}{x+1} =m \ \ \ \ (2.5)$.
Giải
a) Đồ thị

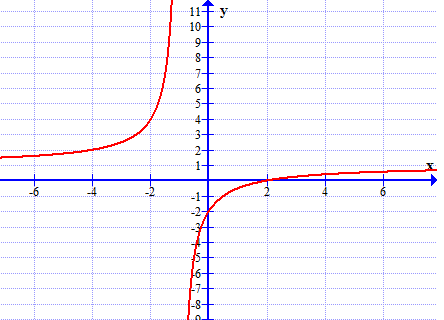
b) Đặt $f(x)=\frac{x-2}{x+1}$. Ta có:$$g(x)=\frac{|x-2|}{x+1}=\left\{\begin{matrix}f(x)& \textrm{khi }x \geq 2\\- f(x)& \textrm{khi }x < 2\\ \end{matrix}\right.$$
Từ đó, để vẽ đồ thị $y=g(x)$, ta làm như sau:
– Giữ nguyên phần đồ thị $\left ( C \right )$ ở bên phải đường thẳng $x=2$
– Lấy đối xứng phần đồ thị $\left ( C \right )$ ở bên trái đường thẳng $x=2$ qua $Ox$
– Xóa bỏ phần đồ thị $\left ( C \right )$ ở bên trái đường thẳng $x=2$
Đồ thị hàm số $y=g(x)$ chính là đường cong màu xanh trong hình vẽ

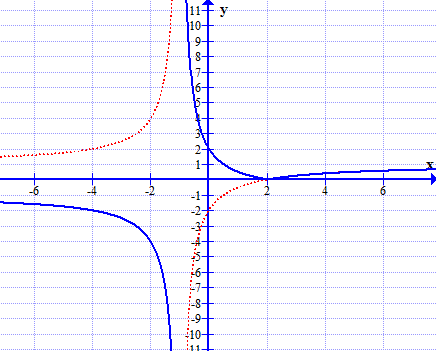
Số nghiệm của phương trình $(2.5)$ bằng số giao điểm của đồ thị hàm số $y=g(x)$ và đường thẳng $y=m$. Ta có các trường hợp sau:
* TH1: Nếu $m < – 1$ hoặc $m\geq 1$ thì phương trình $(2.5)$ có 1 nghiệm.
* TH2: Nếu $-1 \leq m <0$ thì phương trình vô nghiệm
* TH3: Nếu $2 \leq m < 1$ thì phương trình có 2 nghiệm

2. Tìm giao điểm 2 đường và có tham số m:

Ví dụ 1: Tìm giao điểm của đồ thị \((C):y = {x^3} – 3{x^2} + 2x + 1\) và đường thẳng \(y = 1\).

Phương trình hoành độ giao điểm: \({x^3} – 3{x^2} + 2x + 1 = 1 \Leftrightarrow {x^3} – 3{x^2} + 2x = 0\)\( \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 1\\x = 2\end{array} \right.\). Vậy có ba giao điểm \(A\left( {0;1} \right),B\left( {1;1} \right),C\left( {2;1} \right).\)

Ví dụ 2: Cho hàm số \(y = m{x^3} – {x^2} – 2x + 8m\) có đồ thị là \(\left( {{C_m}} \right)\). Tìm m đồ thị \(\left( {{C_m}} \right)\)cắt trục hoành tại ba điểm phân biệt.

Phương trình hoành độ giao điểm \(m{x^3} – {x^2} – 2x + 8m = 0\) (1)
\( \Leftrightarrow \)\(\left( {x + 2} \right)\left[ {m{x^2} – (2m + 1)x + 4m} \right] = 0\)\( \Leftrightarrow \)\(\left[ \begin{array}{l}x = – 2\\m{x^2} – (2m + 1)x + 4m = 0{\rm{ (2)}}\end{array} \right.\)
\(\left( {{C_m}} \right)\) cắt trục hoành tại ba điểm phân biệt \( \Leftrightarrow \)\(\left( 1 \right)\)có ba nghiệm phân biệt.
\( \Leftrightarrow \)\(\left( 2 \right)\)có hai nghiệm phân biệt khác \( – 2\)
\( \Leftrightarrow \)\(\left\{ \begin{array}{l}m \ne 0\\\Delta = – 12{m^2} + 4m + 1 > 0\\12m + 2 \ne 0\end{array} \right.\)
\( \Leftrightarrow \) \(\left\{ \begin{array}{l}m \ne 0\\ – \frac{1}{6} < m < \frac{1}{2}\\m \ne – \frac{1}{6}\end{array} \right.\) \( \Leftrightarrow \)\(\left\{ \begin{array}{l}m \ne 0\\ – \frac{1}{6} < m < \frac{1}{2}\end{array} \right.\).
Vậy \(m \in \left( { – \frac{1}{6};\frac{1}{2}} \right)\backslash \left\{ 0 \right\}\) thỏa yêu cầu bài toán.

Ví dụ 3: Cho hàm số \(y = 2{x^3} – 3m{x^2} + \left( {m – 1} \right)x + 1\) có đồ thị \(\left( C \right)\). Tìm m để đường thẳng \(d:y = – x + 1\) cắt đồ thị \(\left( C \right)\) tại ba điểm phân biệt.

Phương trình hoành độ giao điểm của \(\left( C \right)\)và d:
\(2{x^3} – 3m{x^2} + \left( {m – 1} \right)x + 1 = – x + 1 \Leftrightarrow x\left( {2{x^2} – 3mx + m} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\2{x^2} – 3mx + m = 0\left( * \right)\end{array} \right.\)
Yêu cầu bài toán \( \Leftrightarrow \left( * \right)\) có hai nghiệm phân biệt khác 0
\( \Leftrightarrow \left\{ \begin{array}{l}\Delta = 9{m^2} – 8m > 0\\m \ne 0\end{array} \right.\)
\( \Leftrightarrow m \in \left( { – \infty ;0} \right) \cup \left( {\frac{8}{9}; + \infty } \right)\).
Vậy \(m \in \left( { – \infty ;0} \right) \cup \left( {\frac{8}{9}; + \infty } \right)\) thỏa yêu cầu bài toán.

Ví dụ 4. Cho hàm số \(y = \frac{{2x – 1}}{{x – 1}}\) có đồ thị là (C). Tìm m để đường thẳng \(d:y = – x + m\) cắt đồ thị (C) tại hai điểm phân biệt.

Phương trình hoành độ giao điểm: \(\frac{{2x – 1}}{{x – 1}} = – x + m\) \(\left( 1 \right)\)
Điều kiện: \(x \ne 1\). Khi đó \((1)\) \( \Leftrightarrow \) \(2x – 1 = \left( { – x + m} \right)\left( {x – 1} \right)\)
\( \Leftrightarrow \) \({x^2} – \left( {m – 1} \right)x + m – 1 = 0\) \(\left( 2 \right)\)
dcắt (C)tại hai điểm phân biệt \( \Leftrightarrow \)\(\left( 1 \right)\)có hai nghiệm phân biệt
\( \Leftrightarrow \)(2) có hai nghiệm phân biệt khác \(1\)\( \Leftrightarrow \) \(\left\{ \begin{array}{l}\Delta = {\left[ { – \left( {m – 1} \right)} \right]^2} – 4\left( {m – 1} \right) > 0\\1 – \left( {m – 1} \right).1 + m – 1 \ne 0\end{array} \right.\)
\( \Leftrightarrow \)\({m^2} – 6m + 5 > 0\)\( \Leftrightarrow m \in \left( { – \infty ;1} \right) \cup \left( {5; + \infty } \right).\)
Vậy giá trị m cần tìm là \(m \in \left( { – \infty ;1} \right) \cup \left( {5; + \infty } \right).\)

Ví dụ 5: Cho hàm số \(y = \frac{{mx – 1}}{{x + 2}}\) có đồ thị là \(\left( {{C_m}} \right)\). Tìm m để đường thẳng \(d:y = 2x – 1\) cắt đồ thị \(\left( {{C_m}} \right)\) tại hai điểm phân biệt \(A,{\rm{ }}B\) sao cho \(AB = \sqrt {10} \).

Phương trình hoành độ giao điểm: \(\frac{{mx – 1}}{{x + 2}} = 2x – 1\) \(\left( 1 \right)\)
Điều kiện: \(x \ne – 2\). Khi đó
\((1)\)\( \Leftrightarrow \)\(mx – 1 = \left( {2x – 1} \right)\left( {x + 2} \right)\)\( \Leftrightarrow \)\(2{x^2} – \left( {m – 3} \right)x – 1 = 0\) \(\left( 2 \right)\)
d cắt \(\left( {{C_m}} \right)\)tại hai điểm phân biệt \(A,{\rm{ }}B\) \( \Leftrightarrow \)\(\left( 1 \right)\)có hai nghiệm phân biệt
\( \Leftrightarrow \)(2) có hai nghiệm phân biệt khác \( – 2\)
\( \Leftrightarrow \)\(\left\{ \begin{array}{l}\Delta = {\left[ { – \left( {m – 3} \right)} \right]^2} + 8 > 0\\8 + 2m – 6 – 1 \ne 0\end{array} \right.\) \( \Leftrightarrow \)\(m \ne – \frac{1}{2}\) (*)
Đặt \(A\left( {{x_1};2{x_1} – 1} \right);{\rm{ }}B\left( {{x_2};2{x_2} – 1} \right)\)với \({x_1},{\rm{ }}{x_2}\) là hai nghiệm của phương trình \(\left( 2 \right)\).
Theo định lý Viet ta có \(\left\{ \begin{array}{l}{x_1} + {x_2} = \frac{{m – 3}}{2}\\{x_1}{x_2} = – \frac{1}{2}\end{array} \right.\), khi đó
\(AB = \sqrt {{{\left( {{x_1} – {x_2}} \right)}^2} + 4{{\left( {{x_1} – {x_2}} \right)}^2}} = \sqrt {10} \)\( \Leftrightarrow \)\(5\left[ {{{\left( {{x_1} + {x_2}} \right)}^2} – 4{x_1}{x_2}} \right] = 10\)
\( \Leftrightarrow \)\({\left( {\frac{{m – 3}}{2}} \right)^2} + 2 = 2\)\( \Leftrightarrow \)\(m = 3\) (thỏa (*))
Vậy giá trị m cần tìm là \(m = 3\).

Ví dụ 6: Cho hàm số \(y = \frac{{2x + 1}}{{x + 1}}\) (C). Tìm m để đường thẳng \(d:y = – 2x + m\) cắt (C) tại hai điểm phân biệt \(A,{\rm{ }}B\) sao cho tam giác \(OAB\) có diện tích là \(\sqrt 3 \).

Phương trình hoành độ giao điểm của (C) và d:
\(\frac{{2x + 1}}{{x + 1}} = – 2x + m \Leftrightarrow 2x + 1 = \left( {x + 1} \right)\left( { – 2x + m} \right)\) ( điều kiện: \(x \ne – 1\))
\( \Leftrightarrow 2{x^2} + \left( {4 – m} \right)x + 1 – m = 0{\rm{ }}\left( 1 \right)\) ( điều kiện: \(x \ne – 1\)).
d cắt (C) tại hai điểm\(A,{\rm{ }}B\) phân biệt \( \Leftrightarrow \)(1) có hai nghiệm phân biệt khác \( – 1\).
\( \Leftrightarrow \left\{ \begin{array}{l}\Delta = {m^2} + 8 > 0{\rm{ }}\forall m\\2.{\left( { – 1} \right)^2} + \left( {4 – m} \right)\left( { – 1} \right) + 1 – m \ne 0\end{array} \right.\).
Suy ra d luôn cắt (C) tại hai điểm \(A,{\rm{ }}B\) phân biệt với mọi m.
Gọi \(A\left( {{x_1};{y_1}} \right);{\rm{ }}B\left( {{x_2};{y_2}} \right)\), trong đó\({y_1} = – 2x{}_1 + m;{\rm{ }}{y_2} = – 2x{}_2 + m\) và \({x_1},{\rm{ }}{x_2}\) là các nghiệm của \(\left( 1 \right)\). Theo định lý Viet ta có \(\left\{ \begin{array}{l}{x_1} + {x_2} = \frac{{m – 4}}{2}\\{x_1}{x_2} = \frac{{1 – m}}{2}\end{array} \right.\). Tính được:
\(d\left( {O;AB} \right) = \frac{{\left| m \right|}}{{\sqrt 5 }};{\rm{ }}AB = \sqrt {{{\left( {{x_1} – {x_2}} \right)}^2} + {{\left( {{y_1} – {y_2}} \right)}^2}} = \sqrt {5{{\left( {{x_1} + {x_2}} \right)}^2} – 20{x_1}{x_2}} = \frac{{\sqrt {5\left( {{m^2} + 8} \right)} }}{2}\)
\({S_{OAB}} = \frac{1}{2}AB.d\left( {O;AB} \right) = \frac{{\left| m \right|\sqrt {{m^2} + 8} }}{4} = \sqrt 3 \Leftrightarrow m = 2 \vee m = – 2.\)
Vậy các giá trị m cần tìm là \(m = 2;{\rm{ }}m = – 2.\)