Ứng dụng tích phân tính thể tích khối tròn xoay

Lý thuyết:

• Hàm số  \(y=f(x)\) liên tục và không âm trên \([a,b].\) Hình phẳng giới hạn bởi đồ thị hàm số \(y=f(x)\), trục hoành và hai đường thẳng \(x=a,x=b\) quay quanh trục hoành tạo nên một khối tròn xoay. Thể tích V được tính bởi công thức \(V = \pi \int\limits_a^b {{f^2}(x)dx} .\)

 

• Cho hai hàm số  \(y=f(x)\), \(y=g(x)\) thỏa \(0\leq g(x)\leq f(x)\), liên tục và không âm trên \([a,b].\) Hình phẳng giới hạn bởi đồ thị hàm số \(y=f(x)\), \(y=g(x)\) và hai đường thẳng \(x=a,x=b\) quay quanh trục hoành tạo nên một khối tròn xoay. Thể tích V được tính bởi công thức \(V = \pi \int\limits_a^b {\left[ {{f^2}(x) – {g^2}(x)} \right]dx}.\)
• Cho hai hàm số hình phẳng giới hạn bởi đồ thị hàm số  \(y=f(x)\) và \(y=g(x)\)​ quay quanh trục hoành hoành tạo nên một khối tròn xoay. Để tính được thể tích khối tròn xoay ta thực hiện các bước:
  • Giải phương trình \(f(x) = g(x) \Leftrightarrow \left[ \begin{array}{l} x = a\\ x = b \end{array} \right.\) (Thường dạng bài này đề bài cho phương trình hoành độ giao điểm có hai nghiệm phân biệt).
  • Giải sử \(0\leq g(x)\leq f(x)\) với mọi x thuộc \([a,b].\) Khi đó: \(V = \pi \int\limits_a^b {\left[ {{f^2}(x) – {g^2}(x)} \right]dx}.\)

Bài tập minh họa

Ví dụ 1:

Tính thể tích của phần vật thể giới hạn bởi hai mặt phẳng \(x=0\) và \(x=3\) , có thiết diện bị cắt bởi mặt phẳng vuông góc với trục \(Ox\) tại điểm có hoành độ \(x\left( {0 \le x \le 3} \right)\) là một hình chữ nhật có hai kích thước bằng \(x\) và \(2\sqrt {9 – {x^2}}.\)

Lời giải:

Diện tích của hình chữ nhật có hai cạnh là \(x;2\sqrt {9 – {x^2}}\) là \(2x\sqrt {9 – {x^2}}\)

Khi đó, thể tích của vật thể được xác định bằng công thức \(V = \int\limits_0^3 {2x\sqrt {9 – {x^2}} dx}\)

Đặt \(t = \sqrt {9 – {x^2}} \Leftrightarrow {t^2} = 9 – {x^2} \Leftrightarrow xdx = – tdt\) và \(\left\{ {\begin{array}{*{20}{c}} {x = 0 \Rightarrow t = 3}\\ {x = 3 \Rightarrow t = 0} \end{array}} \right.\)

Suy ra \(V = – 2\int\limits_3^0 {{t^2}dt} = \frac{{2{t^3}}}{3}\left| {\begin{array}{*{20}{c}} 3\\ 0 \end{array}} \right. = 18.\)

Ví dụ 2:

Tính thể tích khối tròn xoay tạo thành khi cho hình phẳng giới hạn bởi đồ thị hàm số \(y = 2x – {x^2}\) và \(y = x\) quay quanh trục Ox.

Lời giải:

Phương trình hoành độ giao điểm của đồ thị hàm số \(y = 2x – {x^2}\) và đường thẳng \(y=x\) là \(2x – {x^2} = x \Leftrightarrow {x^2} – x = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {x = 0}\\ {x = 1} \end{array}} \right.\)

Khi đó, thể tích khối tròn xoay cần tìm là \(V = \pi \int\limits_0^1 {\left| {{{\left( {2x – {x^2}} \right)}^2} – {x^2}} \right|dx} = \pi \int\limits_0^1 {\left| {{x^4} – 4{x^3} + 3{x^2}} \right|dx}\)

\(\Rightarrow V = \left| {\pi \int\limits_0^1 {\left( {{x^4} – 4{x^3} + 3{x^2}} \right)dx} } \right| = \pi \left| {\left( {\frac{{{x^5}}}{5} – {x^4} + {x^3}} \right)\left| {\begin{array}{*{20}{c}} 1\\ 0 \end{array}} \right.} \right| = \frac{\pi }{5}.\)

---

Ví dụ 3: (Đề tham khảo 2018)

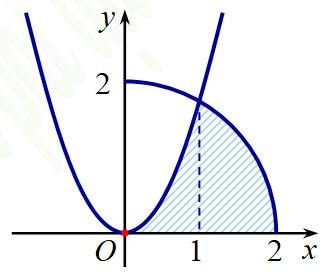
Câu 31. Cho hình $(H)$ là hình phẳng giới hạn bởi parabol $y=\sqrt3x^2$, cung tròn có phương trình $y=\sqrt{4-x^2}$ (với $0\le x\le 2$) và trục hoành (phần tô đậm trong hình vẽ).

Diện tích của $(H)$ bằng

A. $\dfrac{4\pi+\sqrt3}{12}$.          B. $\dfrac{4\pi-\sqrt3}{12}$.

C. $\dfrac{4\pi+2\sqrt3-3}6$.         D. $\dfrac{5\sqrt3-2\pi}3$.

Lời giải

Ta có:
$\sqrt{3}{{x}^{2}}=\sqrt{4-{{x}^{2}}}\Leftrightarrow 3{{x}^{4}}+{{x}^{2}}-4=0\Leftrightarrow \left( {{x}^{2}}-1 \right)\left( {{x}^{2}}+4 \right)=0$

$\Leftrightarrow \left[ \begin{array}{ll}
x=1&(nhan) \\
x=-1&(loai) \\
\end{array} \right.$
Do đó:
$S = \displaystyle\int_0^1 {\sqrt 3 {x^2}{\rm d}x} + \int_1^2 {\sqrt {4 – {x^2}} {\rm d}x}$

$= {\dfrac{{\sqrt 3 }}{3}{x^3}} \bigg|_0^1 + \int_1^2 {\sqrt {4 – {x^2}} {\rm d}x}$

$= \dfrac{{\sqrt 3 }}{3} + \int_1^2 {\sqrt {4 – {x^2}} {\rm d}x}$
Tính $I = \displaystyle\int_1^2 {\sqrt {4 – {x^2}} {\rm d}x}$ .
Đặt $x = 2\sin t \Rightarrow {\rm d}x = 2\cos t{\rm d}t$.
Đổi cận $\left\{ \begin{array}{l}x = 1 \Rightarrow \sin t = \dfrac{1}{2} \Rightarrow t = \dfrac{\pi }{6}\\x = 2 \Rightarrow \sin t = 1 \Rightarrow t = \dfrac{\pi }{2}\end{array} \right.$
$I = \int_1^2 {\sqrt {4 – {x^2}} {\rm d}x} = \int_{\pi /6}^{\pi /2} {\sqrt {4 – 4{{\sin }^2}t} .2\cos t{\rm d}t} $

$= \int_{\pi /6}^{\pi /2} {4{{\cos }^2}t{\rm d}t} = \int_{\pi /6}^{\pi /2} {2\left( {\cos 2t + 1} \right){\rm d}t}$

$= {\sin 2t} \Bigg|_{\pi /6}^{\pi /2} + {2t} \Bigg|_{\pi /6}^{\pi /2} = \dfrac{{2\pi }}{3} – \dfrac{{\sqrt 3 }}{2}$
Suy ra $S = \dfrac{{\sqrt 3 }}{3} + \dfrac{{2\pi }}{3} – \dfrac{{\sqrt 3 }}{2} = \dfrac{{4\pi – \sqrt 3 }}{6}$.
————
Ví dụ 4: Tính thể tích khối tròn xoay khi quay quanh Ox
a) Đồ thị hàm số y = sinx, trục hoành, đường thẳng x = $\frac{\pi }{2}$, x =$\pi $
Ta có: $V=\pi \int\limits_{\frac{\pi }{2}}^{\pi }{{{\sin }^{2}}xdx=\frac{\pi }{2}\int\limits_{\frac{\pi }{2}}^{\pi }{\left( 1-\cos 2x \right)}}dx$

$=\frac{\pi }{2}\left( x-\frac{1}{2}\sin 2x \right)\left| _{\frac{\pi }{2}}^{\pi } \right.$

$=\frac{\pi }{2}\left( \pi -\frac{\pi }{2} \right)=\frac{{{\pi }^{2}}}{4}$ (ĐVTT)
b) Đồ thị hàm số y = cosx, y = 0, x = 0 , x = $\frac{\pi }{4}$
Ta có: V = $\pi \int\limits_{0}^{\frac{\pi }{4}}{{{\cos }^{2}}xdx}=\frac{\pi }{2}\int\limits_{0}^{\frac{\pi }{4}}{(1+\cos 2x)dx}$

$=\frac{\pi }{2}\left. \left( x+\frac{1}{2}\sin 2x \right) \right|_{0}^{\frac{\pi }{4}}=\frac{\pi }{2}\left( \frac{\pi }{4}+\frac{1}{2} \right)$(ĐVTT)
c) Đồ thị hàm số y =$x.{{e}^{x}}$ , y = 0, x = 0, x = 1
Ta có : V = $\pi \int\limits_{0}^{1}{{{x}^{2}}{{e}^{2x}}dx}$

Đặt : $\left\{\begin{matrix}
u={{x}^{2}} & \\
dv={{e}^{2x}}dx &
\end{matrix}\right. \Rightarrow \left\{ \begin{matrix}
du=2xdx & \\
v=\frac{1}{2}{{e}^{2x}} &
\end{matrix} \right.$
V = $\frac{\pi }{2}\left. {{x}^{2}}{{e}^{2x}} \right|_{0}^{1}-\pi \int\limits_{0}^{1}{x{{e}^{x}}dx}$

$=\frac{\pi }{2}.{{e}^{2}}-\pi \int\limits_{0}^{1}{x.{{e}^{2x}}dx}$
Tính I = $\int\limits_{0}^{1}{x.{{e}^{2x}}dx}$

Đặt $\left\{ \begin{matrix}
u=x & \\
dv={{e}^{2x}}dx &
\end{matrix} \right. \Rightarrow \left\{ \begin{matrix}
du=dx & \\
v=\frac{1}{2}{{e}^{2x}} &
\end{matrix} \right.$
$\Rightarrow \frac{x}{2}e^{2x} |_{0}^{1} -\frac{1}{2} \int\limits_{0}^{1}{e}^{2x}dx$

$= \frac{1}{2}e^2-\frac{1}{4}{{e}^{2x}} |_{0}^{1}=\frac{1}{2}{{e}^{2}}-\frac{1}{4}{{e}^{2}}+\frac{1}{4}$
Thay I vào V

ta có : V = $\frac{\pi }{2}.{{e}^{2}}-\pi \int\limits_{0}^{1}{x.{{e}^{2x}}dx}$

$=\frac{\pi {{e}^{2}}}{2}-\pi \left( \frac{{{e}^{2}}}{2}-\frac{{{e}^{2}}}{4}+\frac{1}{4} \right)=\frac{\pi }{4}\left( {{e}^{2}}-1 \right)$(ĐVTT)
d) Đồ thị hàm số : $y=\frac{1}{3}{{x}^{3}}-{{x}^{2}}$ và các đường y = 0, x = 0, x = 3.
V = $\pi \int\limits_{0}^{3}( \frac{1}{3}{x}^{3}-{x}^{2})^2dx$

$=\pi \int\limits_{0}^{3}( \frac{1}{9}{x}^{6}-\frac{2}{3}{x}^{5}+{x}^{4})dx$

$=\pi \left( \frac{{{x}^{7}}}{63}-\frac{{{x}^{6}}}{9}+\frac{{{x}^{5}}}{5} \right)\left| _{0}^{3} \right.=\frac{81\pi }{35}$( ĐVTT)