Từ tấm bìa hình vuông có cạnh bằng $6$ người ta cắt bỏ các tam giác vuông cân tạo thành hình tô đậm như hình vẽ

Từ tấm bìa hình vuông có cạnh bằng $6$ người ta cắt bỏ các tam giác vuông cân tạo thành hình tô đậm như hình vẽ. Sau đó người ta gập thành hình hộp chữ nhật không nắp. Thể tích lớn nhất của khối hộp chữ nhật bằng bao nhiêu ?

Đáp án: 11,3

Lời giải: Gọi cạnh hình tam giác cân bị cắt bỏ ở bốn góc của tấm bìa có độ dài là $x$.

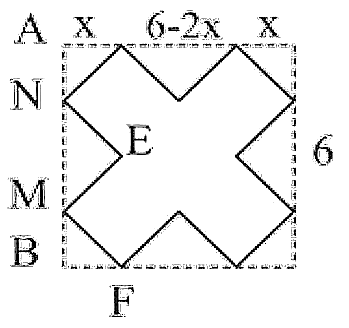
Ta có: $AN=BM=x\Rightarrow MN=6-2x$.
$\Rightarrow EM=EN=\dfrac{6-2x}{\sqrt{2}}$.
Hình hộp chữ nhật không nắp có đáy là hình vuông cạnh $MF=x\sqrt{2}$,và có chiều cao $EN=\dfrac{6-2x}{\sqrt{2}}$.
Suy ra $V=M{{F}^{2}}.EN=2{{x}^{2}}.\dfrac{6-2x}{\sqrt{2}}=\sqrt{2}{{x}^{2}}\left( 6-2x \right)=-2\sqrt{2}{{x}^{3}}+6\sqrt{2}{{x}^{2}}$.
$\Rightarrow {V}’=-6\sqrt{2}{{x}^{2}}+12\sqrt{2}x=0\Leftrightarrow \left[ \begin{array}{*{35}{l}} x=0(l) \\ x=2(n) \end{array} \right.$.

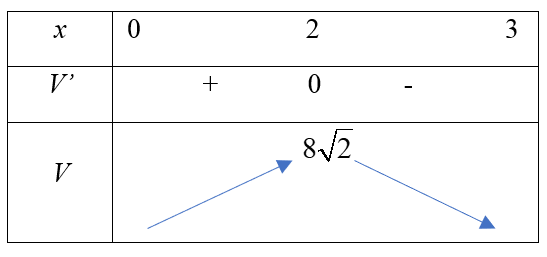
Vậy ${{V}_{\text{max}}}=V\left( 2 \right)=8\sqrt{2}\approx 11,3$.