Từ một tấm tôn có hình dạng là nửa hình tròn bán kính $R=5$, người ta muốn cắt ra một hình chữ nhật

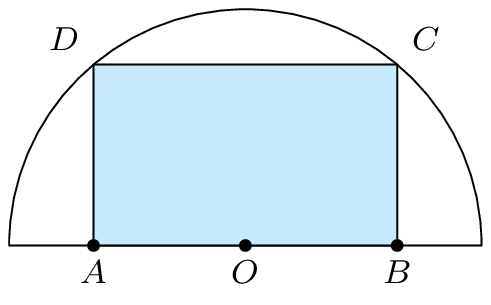
Từ một tấm tôn có hình dạng là nửa hình tròn bán kính $R=5$, người ta muốn cắt ra một hình chữ nhật. Diện tích lớn nhất có thể của tấm tôn hình chữ nhật là bao nhiêu?

Đáp án: 25

Lời giải: Đăt $OA=x\Rightarrow AB=2x$ ( $0{<}x{
$\Rightarrow AD=\sqrt{O{{D}^{2}}-O{{A}^{2}}}=\sqrt{25-{{x}^{2}}}$.
Diện tích hình chữ nhật $ABC\text{D}$ là $S=AB.AD=2x\sqrt{25-{{x}^{2}}}$.
Xét hàm số: $f\left( x \right)=2x\sqrt{25-{{x}^{2}}}$ trên $\left( 0;5 \right)$, ta có
$f’\left( x \right)=2\sqrt{25-{{x}^{2}}}-\dfrac{2{{x}^{2}}}{\sqrt{25-{{x}^{2}}}}$.
$f’\left( x \right)=0\Leftrightarrow \dfrac{50-4{{x}^{2}}}{\sqrt{25-{{x}^{2}}}}=0\Leftrightarrow 50-4{{x}^{2}}=0\Rightarrow \left[ \begin{matrix} x=\dfrac{5\sqrt{2}}{2}\in (0;5) \\ x=\dfrac{-5\sqrt{2}}{2}\notin (0;5) \\ \end{matrix} \right.$.
Bảng biến thiên

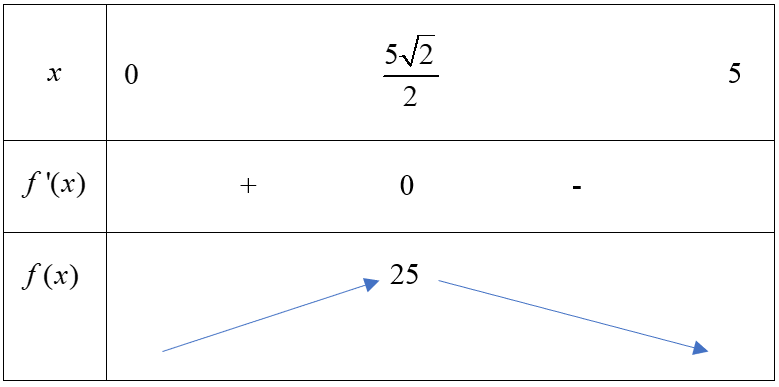
Vậy diện tích lớn nhất của tấm nhôm hình chữa nhật là $S=25$ khi $x=\dfrac{5\sqrt{2}}{2}$.