Từ một khúc gỗ tròn hình trụ có đường kính bằng 40 cm, cần xả thành một chiếc xà có tiết diện ngang là hình vuông và bốn miếng phụ được tô màu xám như hình vẽ dưới đây

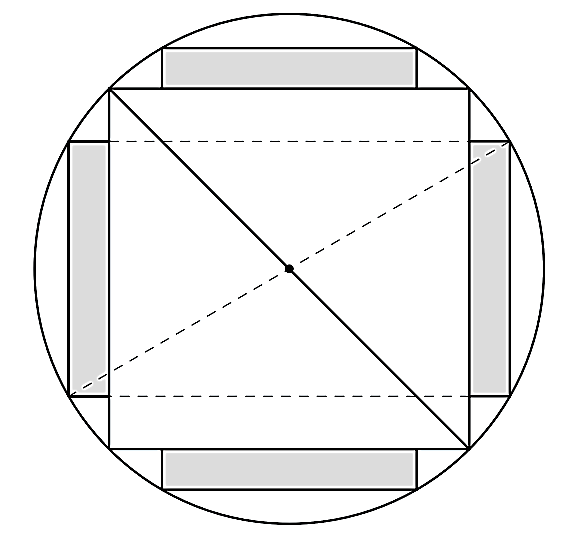
Từ một khúc gỗ tròn hình trụ có đường kính bằng 40 cm, cần xả thành một chiếc xà có tiết diện ngang là hình vuông và bốn miếng phụ được tô màu xám như hình vẽ dưới đây. Tìm chiều rộng $x$ của miếng phụ để diện tích sử dụng theo tiết diện ngang là lớn nhất. (làm tròn kết quả đến hàng phần trăm).

Đáp án: 3,97

Lời giải:

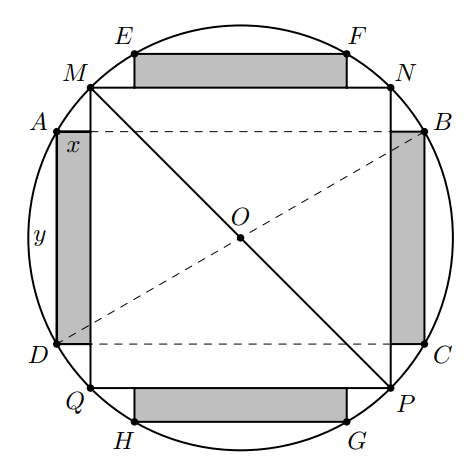
Gọi $y$ là chiều dài của miếng phụ.
Diện tích sử dụng theo tiết diện ngang là $S=S_{M N P Q}+4 x y$.
Cạnh hình vuông $M N=\dfrac{M P}{\sqrt{2}}=\dfrac{40}{\sqrt{2}}=20 \sqrt{2}$ cm $\Rightarrow S=(20 \sqrt{2})^2+4 x y=800+4 x y$
Ta có $2 x=A B-M N=A B-20 \sqrt{2}{<}x{
Lại có $A B^2+A D^2=B D^2=40^2 \Rightarrow(2 x+20 \sqrt{2})^2+y^2=1600$.
Thế vào (1), ta được
$S =800+4 x \sqrt{800-80 x \sqrt{2}-4 x^2} =800+4 \sqrt{800 x^2-80 x^3 \sqrt{2}-4 x^4}$
Xét hàm số $f(x)=800 x^2-80 x^3 \sqrt{2}-4 x^4$, với $x \in(0 ; 20-10 \sqrt{2})$ có
$f^{\prime}(x)=1600 x-240 x^2 \sqrt{2}-16 x^3=16 x\left(100-15 x \sqrt{2}-x^2\right)$.
Ta có bảng biến thiên

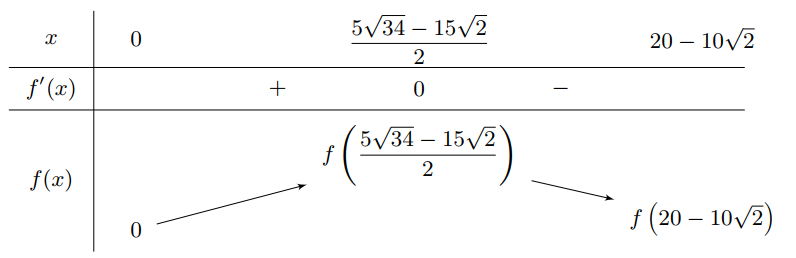
Vậy $x=\dfrac{5 \sqrt{34}-15 \sqrt{2}}{2} \approx 3,97$ chính là giá trị cần tìm.