Trong thống kê tại một chuỗi nhà máy của công ty X, nếu áp dụng tuần làm việc 40 giờ thì mỗi tuần có 100 tổ công nhân đi làm và mỗi tổ làm được 120 sản phẩm trong một giờ. Nếu tăng thời gian làm việc thêm 2 giờ mỗi tuần sẽ có thêm 1 tổ nghỉ việc và năng suất lao động giảm 5 sản phẩm/1 tổ/1 giờ (và như vậy, nếu giảm thời gian làm việc 2 giờ mỗi tuần thì sẽ có thêm 1 tổ công nhân đi làm và năng suất lao động tăng 5 sản phẩm/1 tổ/1 giờ). Ngoài ra, số phế phẩm mỗi tuần ước tính là $P\left( x \right)=\dfrac{95{{x}^{2}}+120x}{4}$, với $x$ là thời gian (tính bằng giờ) làm việc trong một tuần. Công ty cần áp dụng thời gian làm việc mấy giờ mỗi tuần để số lượng sản phẩm thu được hàng tuần là lớn nhất?
Đáp án: 36
Lời giải: Gọi $t$ là số giờ làm tăng thêm mỗi tuần (tính bằng giờ), $t\in \mathbb{Z},t$ chia hết cho 2.
Với $t{>}0$ thì số giờ làm tăng thêm, $t{
Số tổ công nhân bỏ việc (hoặc tăng thêm) là $\dfrac{t}{2}$ nên số tổ công nhân làm việc là $100-\dfrac{t}{2}$ (tổ).
Năng suất của mỗi tổ công nhân còn $120-\dfrac{5t}{2}$ sản phẩm một giờ.
Số thời gian làm việc 1 tuần là $40+t$ nên số sản phẩm đạt được trong một tuần làm việc là:
$\left( 100-\dfrac{t}{2} \right)\left( 120-\dfrac{5t}{2} \right)\left( 40+t \right)$.
Số sản phầm thu được là $f\left( t \right)=\left( 100-\dfrac{t}{2} \right)\left( 120-\dfrac{5t}{2} \right)\left( 40+t \right)-\dfrac{95{{\left( 40+t \right)}^{2}}+120\left( 40+t \right)}{4}$.
Điều kiện $\left\{ \begin{array}{l} 120-\dfrac{5t}{2}{>}0 \\ 100-\dfrac{t}{2}{>}0 \\ 40+t{>}0 \end{array} \right.\Leftrightarrow -40{<}t{
Ta có ${f}’\left( t \right)=-\dfrac{1}{2}\left( 120-\dfrac{5t}{2} \right)\left( 40+t \right)-\dfrac{5}{2}\left( 100-\dfrac{t}{2} \right)\left( 40+t \right)+\left( 100-\dfrac{t}{2} \right)\left( 120-\dfrac{5t}{2} \right)-\dfrac{95}{2}\left( 40+t \right)-30$
$=\dfrac{15{{t}^{2}}}{4}-\dfrac{1135t}{2}-2330$.
${f}’\left( t \right)=0\Leftrightarrow \left[ \begin{array}{l} t=-4 \\ t=\dfrac{466}{3} \end{array} \right.$.
Kết hợp điều kiện suy ra $t=-4$. Ta có bảng biến thiên của hàm số $f\left( t \right)$ trên khoảng $\left( -40;48 \right)$ như sau:
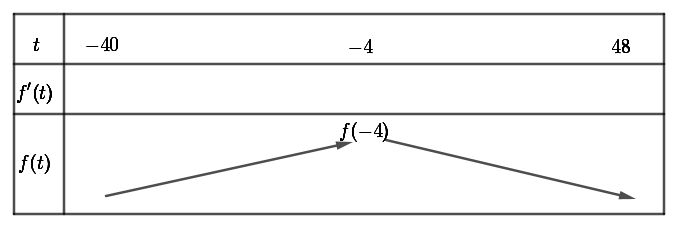
Khi $t=-4$ thì $x=40-4=36$
Vậy số lượng sản phẩm thu được mỗi tuần lớn nhất khi thời gian làm việc là 36 giờ mỗi tuần.
