Trong phòng thí nghiệm người ta xác định được số lượng vi khuẩn được nuôi cấy tính theo công thức $N\left( t \right)=1000+\dfrac{100t}{100+{{t}^{2}}}$ (con vi khuẩn)

Trong phòng thí nghiệm người ta xác định được số lượng vi khuẩn được nuôi cấy tính theo công thức $N\left( t \right)=1000+\dfrac{100t}{100+{{t}^{2}}}$ (con vi khuẩn). Tính số lượng vi khuẩn lớn nhất kể từ khi nuôi cấy.
Đáp án: 7

Lời giải: Tốc độ thay đổi số lượng ong của đàn theo thời gian $t$ là $T\left( t \right)={P}’\left( t \right)={{2.10}^{7}}\cdot \dfrac{{{e}^{-t}}}{{{\left( 1+1000{{e}^{-t}} \right)}^{2}}}$.
Ta có:
$\begin{array}{*{35}{r}} {T}’\left( t \right) =2\cdot {{10}^{7}}\cdot \dfrac{-{{e}^{-t}}\cdot {{\left( 1+1000{{e}^{-t}} \right)}^{2}}-{{e}^{-t}}\cdot 2\cdot \left( 1+1000{{e}^{-t}} \right)\cdot \left( -1000{{e}^{-t}} \right)}{{{\left( 1+1000{{e}^{-t}} \right)}^{4}}} \\ {} ={{2.10}^{7}}\cdot \dfrac{{{e}^{-t}}\left( 1000{{e}^{-t}}-1 \right)}{{{\left( 1+1000{{e}^{-t}} \right)}^{3}}}=2\cdot {{10}^{7}}\cdot \dfrac{{{e}^{-2t}}\left( 1000-{{e}^{t}} \right)}{{{\left( 1+1000{{e}^{-t}} \right)}^{3}}} \end{array}$
${T}’\left( t \right)=0\Leftrightarrow 1000-{{e}^{t}}=0\Leftrightarrow t=\text{ln}1000$.
Bảng xét dấu của đạo hàm:

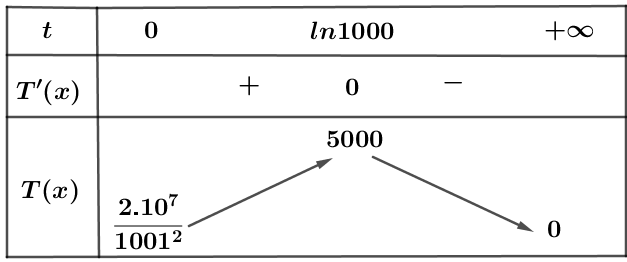
Từ đó, $T\left( t \right)$ đạt giá trị lớn nhất tại $t=\text{ln}1000\approx 7$.
Vậy đàn ong tăng nhanh nhất tại thời điểm khoảng $t=7$ tuần.