Trong một thí nghiệm y học, người ta cấy 1000 vi khuẩn vào môi trường dinh dưỡng

Trong một thí nghiệm y học, người ta cấy 1000 vi khuẩn vào môi trường dinh dưỡng. Bằng thực nghiệm, người ta xác định được số lượng vi khuẩn thay đổi theo thời gian bởi công thức: $N\left( t \right)=1000+\dfrac{100t}{100+{{t}^{2}}}(\text{con}),$ trong đó $t$ là thời gian tính bằng giây. Tính số lượng vi khuẩn lớn nhất kể từ khi thực hiện cấy vi khuẩn vào môi trường dinh dưỡng.
Đáp án: 1005

Lời giải: Xét hàm số $N\left( t \right)=1000+\dfrac{100t}{100+{{t}^{2}}}\left( t{>}0 \right)$.
Ta có: ${N}’\left( t \right)=\dfrac{100.\left( 100+{{t}^{2}} \right)-100t.2t}{{{\left( 100+{{t}^{2}} \right)}^{2}}}=\dfrac{100.\left( 100-{{t}^{2}} \right)}{{{\left( 100+{{t}^{2}} \right)}^{2}}}$.
Khi đó, với $t{>}0,{N}’\left( t \right)=0\Leftrightarrow 100-{{t}^{2}}=0\Leftrightarrow {{t}^{2}}=100\Leftrightarrow t=10$.
Bảng biến thiên của hàm số $N\left( t \right)$ như sau:

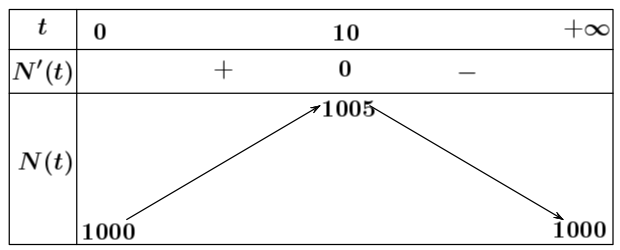
Căn cứ bảng biến thiên, ta thấy:
Trên khoảng $\left( 0;+\infty \right)$ hàm số $N\left( t \right)$ đạt giá trị lớn nhất bằng 1005 tại $t=10$.
Vậy số lượng vi khuẩn lớn nhất kể từ khi thực hiện cấy vi khuẩn vào môi trường dinh dưỡng là 1005 con.