Trong một nhà hàng, mỗi tuần để chế biến $x$ phần thức ăn ( $x$ lấy giá trị trong khoảng từ 30 đến 120) thì người ta tính được chi phí trung bình (đơn vị: nghìn đồng) của một phần ăn được cho bởi công thức: $\overline{C}(x)=2x-230+\dfrac{7200}{x}$

Trong một nhà hàng, mỗi tuần để chế biến $x$ phần thức ăn ( $x$ lấy giá trị trong khoảng từ 30 đến 120) thì người ta tính được chi phí trung bình (đơn vị: nghìn đồng) của một phần ăn được cho bởi công thức: $\overline{C}(x)=2x-230+\dfrac{7200}{x}$. Tìm số phần ăn sao cho chi phí trung bình của một phần ăn là thấp nhất.
Đáp án: 60

Lời giải: Ta khảo sát hàm số $\overline{C}(x)=2x-230+\dfrac{7200}{x}$ với $30{<}x{
$\overline{C}'(x)=2-\dfrac{7200}{{{x}^{2}}}=0\Leftrightarrow x=\pm 60$
Bảng biến thiên:

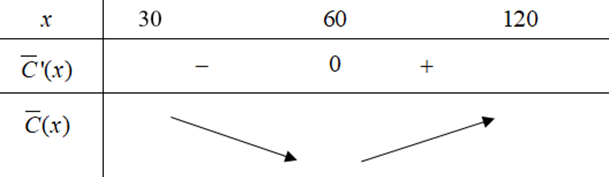
Vậy chi phí trung bình của một phần ăn thấp nhất khi số phần ăn là $x=60$