Trong 5 giây đầu tiên, một chất điểm chuyển động theo phương trình $s\left( t \right)=-{{t}^{3}}+6{{t}^{2}}+t+5$, Trong đó $t$ tính bằng giây và $s$ tính bằng mét

Trong 5 giây đầu tiên, một chất điểm chuyển động theo phương trình $s\left( t \right)=-{{t}^{3}}+6{{t}^{2}}+t+5$, Trong đó $t$ tính bằng giây và $s$ tính bằng mét. Chất điểm có vận tốc tức thời lớn nhất bằng bao nhiêu trong 5 giây đầu tiên đó?
Đáp án: 2

Lời giải: Xét hàm số $s\left( t \right)=-{{t}^{3}}+6{{t}^{2}}+t+5$ $\left( t{>}0 \right)$,
Ta có $v\left( t \right)={s}’\left( t \right)=-3{{t}^{2}}+12t+1$;
Khi đó ${v}’\left( t \right)=-6t+12$;
${v}’\left( t \right)=0\Leftrightarrow -6t+12=0\Leftrightarrow t=2$
Bảng biến thiên của hàm số $v\left( t \right)$ như sau:

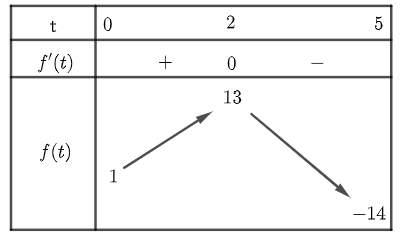
Dựa vào bảng biến thiên, ta thấy $\max\limits_{\left( 0;5 \right]} v\left( t \right)=v\left( 2 \right)=13$.
Vậy vận tốc tức thời của chất điểm lớn nhất bằng $13m/s$ tại $t=2$ giây.