Trong 15 phút theo dõi, lưu lượng nước của một con sông được tính theo công thức:
$Q\left( t \right)=-\dfrac{1}{5}{{t}^{3}}+3{{t}^{2}}+100$

Trong 15 phút theo dõi, lưu lượng nước của một con sông được tính theo công thức:
$Q\left( t \right)=-\dfrac{1}{5}{{t}^{3}}+3{{t}^{2}}+100$. Trong đó $\text{Q}$ được tính theo ${{\text{m}}^{3}}/$ phút, $\text{t}$ tính theo phút, $0\le \text{t}\le 15$.
Trong thời gian theo dõi, lưu lượng nước của con sông lớn nhất bằng bao nhiêu ?
Đáp án: 200

Lời giải: Đáp số: 200.
Xét hàm số $Q\left( t \right)=-\dfrac{1}{5}{{t}^{3}}+3{{t}^{2}}+100$ với $t\in \left[ 0;15 \right]$.
Ta có ${Q}’\left( t \right)=-\dfrac{3}{5}{{t}^{2}}+6t$.
${Q}’\left( t \right)=0\Leftrightarrow -\dfrac{3}{5}{{t}^{2}}+6t=0\Leftrightarrow \left[ \begin{array}{l} t=0 \\ t=10 \end{array} \right.$.
Bảng biến thiên:

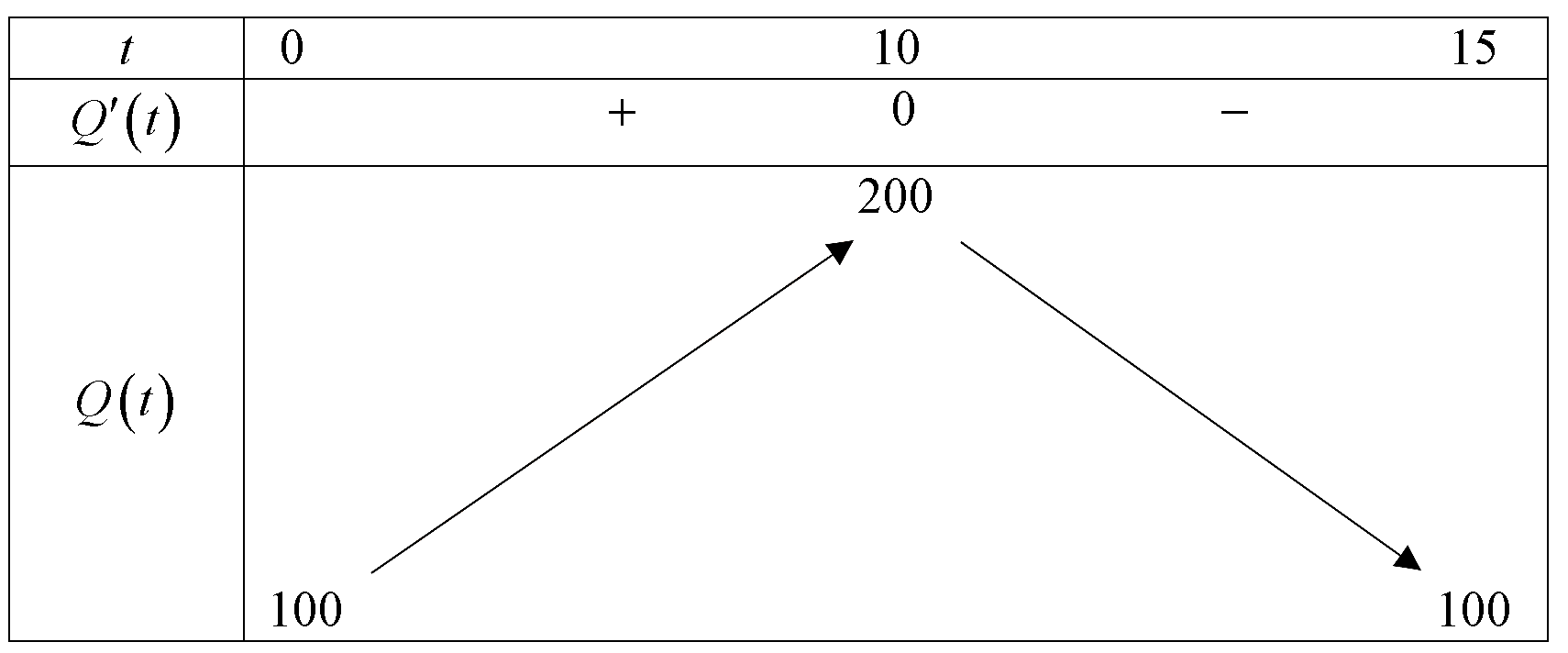
Từ bảng biến thiên suy ra, lưu lượng nước con sông lớn nhất bằng 200 ${{\text{m}}^{3}}/$ phút.