Trên mảnh đất hình chữ nhật $ABCD$ có diện tích $25{{\text{m}}^{2}}$, người chủ lấy một phần đất để trồng cỏ

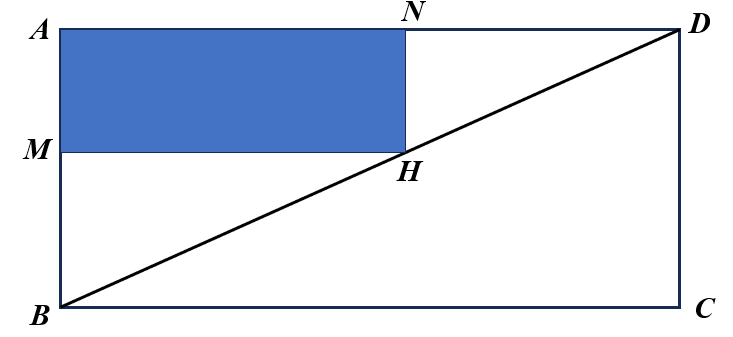
Trên mảnh đất hình chữ nhật $ABCD$ có diện tích $25{{\text{m}}^{2}}$, người chủ lấy một phần đất để trồng cỏ. Biết phần đất trồng cỏ này có dạng hình chữ nhật với hai đỉnh đối diện là $A$ và $H$, với $H$ thuộc cạnh $BD$. Biết chi phí trồng cỏ là $80$ (nghìn đồng) $/{{\text{m}}^{2}}$. Hỏi số tiền lớn nhất người chủ cần chuẩn bị để trồng cỏ (miền tô đậm) là bao nhiêu (nghìn đồng)?

Đáp án: 500

Lời giải: Vì $\Delta DHN$ đồng dạng với $\Delta DBA$ nên $\dfrac{DN}{DA}=\dfrac{NH}{AB}=x$, với $0{<}x{
Khi đó $NH=x.AB$; $DN=x.DA\Rightarrow AN=\left( 1-x \right)DA$.
Ta có ${{S}_{AMHN}}=AN.NH=x\left( 1-x \right).AB.DA=x\left( 1-x \right){{S}_{ABCD}}=25x\left( 1-x \right)$.
Số tiền người chủ cần chuẩn bị để trồng cỏ là $80.25x\left( 1-x \right)$ (nghìn đồng).
Để số tiền lớn nhất thì $f\left( x \right)=x\left( 1-x \right)$ đạt giá trị lớn nhất trên khoảng $\left( 0;1 \right)$.
Nhận thấy $f\left( x \right)=x\left( 1-x \right)=x-{{x}^{2}}=\dfrac{1}{4}-{{\left( \dfrac{1}{2}-x \right)}^{2}}\le \dfrac{1}{4},\forall x\in \left( 0;1 \right)$. Dấu bằng xảy ra khi và chỉ khi $x=\dfrac{1}{2}$.
Vậy số tiền lớn nhất người chủ cần chuẩn bị để trồng cỏ là $500$ (nghìn đồng).