Bài toán gốc Cho hàm số $y=f\left( x \right)=\dfrac{{{x}^{2}}}{x-2}$ có đồ thị $\left( C \right)$.Các mệnh đề sau là đúng hay sai?a) Đạo hàm của hàm số là $f'(x)=\dfrac{x^{2}-4x}{(x-2)^{2}}$.b) Giá trị cực tiểu của hàm số là $y_{CT}=8$.c) Tâm đối xứng của đồ thị $(C)$ là $I(2;4)$.d) Hàm số $y=f(x)-2x$ đồng biến trên khoảng $(2;+\infty)$.Lời giải: ${f}'\left( x … [Đọc thêm...] vềCho hàm số $y=f\left( x \right)=\dfrac{{{x}^{2}}}{x-2}$ có đồ thị $\left( C \right)$.Các mệnh đề sau là đúng hay sai?
Trắc nghiệm Tiệm cận
Cho hàm số $y=f\left( x \right)$ có đồ thị như hình vẽ.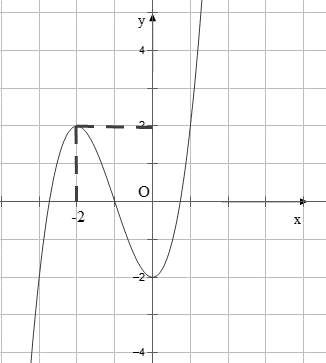

Bài toán gốc Cho hàm số $y=f\left( x \right)$ có đồ thị như hình vẽ.a) Đường thẳng $y=2$ là tiệm cận ngang của đồ thị $y=f\left( x \right)$..b) $\lim\limits_{x\to \pm \infty }\dfrac{1}{f\left( x \right)-1}=1$..c) Đồ thị $y=\dfrac{2019}{f\left( x \right)-1}$ có tiệm cận ngang là $y=0$..d) Số tiệm cận đứng của đồ thị hàm số $y=\dfrac{2019}{f\left( x \right)-1}$ là 2..Lời … [Đọc thêm...] vềCho hàm số $y=f\left( x \right)$ có đồ thị như hình vẽ.

Cho hàm số $y=f(x)$ có bảng biến thiên như hình dưới đây: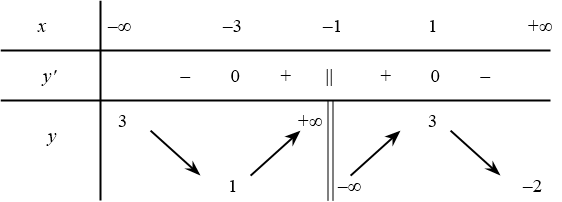

Bài toán gốc Cho hàm số $y=f(x)$ có bảng biến thiên như hình dưới đây:Xét tính đúng sai của các phát biểu sau:a) Đồ thị hàm số $y=f(x)$ có một đường tiệm cận ngang.b) Đồ thị hàm số $y=f(x)$ có tiệm cận ngang là đường thẳng $y=-1$.c) Đồ thị hàm số $y=f(x)$ có tiệm cận đứng là đường thẳng $x=-2$.d) Đồ thị hàm số $y=f(x)$ có tiệm cận đứng là đường thẳng $x=-1$.Lời … [Đọc thêm...] vềCho hàm số $y=f(x)$ có bảng biến thiên như hình dưới đây:

Cho hàm số $y=f(x)=\dfrac{{{x}^{2}}+4x+1}{x+4}\cdot$a) Tập xác định của hàm số đã cho là $D=\mathbb{R}.$.
Bài toán gốc Cho hàm số $y=f(x)=\dfrac{{{x}^{2}}+4x+1}{x+4}\cdot$a) Tập xác định của hàm số đã cho là $D=\mathbb{R}.$.b) Hàm số đã cho không có cực trị.c) Trục đối xứng của đồ thị hàm số đi qua điểm $\left( -4;-4 \right).$.d) Đồ thị hàm số có một đường tiệm cận xiên và một đường tiệm cận đứng.Lời giải: Đúng. ĐKXĐ $x+4\ne 0\Rightarrow$ TXĐ: $D=\mathbb{R}\backslash … [Đọc thêm...] vềCho hàm số $y=f(x)=\dfrac{{{x}^{2}}+4x+1}{x+4}\cdot$
a) Tập xác định của hàm số đã cho là $D=\mathbb{R}.$.
Cho hàm số $(C):y=f(x)=\dfrac{mx-1}{2x-4}$. Khi đóa) Nếu $m=-2$ thì đường thẳng $y=1$ là tiện cận ngang của $(C)$.
Bài toán gốc Cho hàm số $(C):y=f(x)=\dfrac{mx-1}{2x-4}$. Khi đóa) Nếu $m=-2$ thì đường thẳng $y=1$ là tiện cận ngang của $(C)$.b) Đồ thị hàm số đã cho có tiệm cận đứng khi $m\ne \dfrac{1}{2}$.c) Điểm $(2;3)$ là tâm đối xứng của đồ thị hàm số khi $m=6$.d) $\forall m\in \mathbb{R}$ ta có tiệm cận ngang của $(C)$ là đường thẳng $y=\dfrac{m}{2}$.Lời giải:(Sai) Nếu $m=-2$ … [Đọc thêm...] vềCho hàm số $(C):y=f(x)=\dfrac{mx-1}{2x-4}$. Khi đó
a) Nếu $m=-2$ thì đường thẳng $y=1$ là tiện cận ngang của $(C)$.
Cho hàm số $y=\dfrac{x-1}{2x-3}\left( C \right)$
Cho hàm số $y=\dfrac{x-1}{2x-3}\left( C \right)$. Gọi $I$ là giao điểm của hai đường tiệm cận của đồ thị hàm số. Đường thẳng $2x+y-1=0$ cắt tiệm cận đứng tại $A$ và cắt tiệm cận ngang tại $B$. Tính diện tích của tam giác $IAB$, kết quả làm tròn đến hàng phần trăm.Đáp án: 1,56Lời giải: Đồ thị $\left( C \right)$ có đường tiệm cận ngang: $y=\dfrac{1}{2}$; đường tiệm cận đứng: … [Đọc thêm...] vềCho hàm số $y=\dfrac{x-1}{2x-3}\left( C \right)$
Tìm được trên đồ thị $\left( C \right):y=\dfrac{x+2}{x-3}$ những điểm $M$ sao cho khoảng cách từ điểm $M$ đến đường tiệm cận đứng bằng $\dfrac{1}{5}$ khoảng cách từ điểm $M$ đến đường tiệm cận ngang
Tìm được trên đồ thị $\left( C \right):y=\dfrac{x+2}{x-3}$ những điểm $M$ sao cho khoảng cách từ điểm $M$ đến đường tiệm cận đứng bằng $\dfrac{1}{5}$ khoảng cách từ điểm $M$ đến đường tiệm cận ngang. Hỏi có bao nhiêu điểm $M$ thỏa mãn?Đáp án: 2Lời giải: Hàm số đã cho xác định và liên tục trên $\left( -\infty ;3 \right)\cup \left( 3;+\infty \right)$Gọi đường tiệm cận đứng, tiệm … [Đọc thêm...] vềTìm được trên đồ thị $\left( C \right):y=\dfrac{x+2}{x-3}$ những điểm $M$ sao cho khoảng cách từ điểm $M$ đến đường tiệm cận đứng bằng $\dfrac{1}{5}$ khoảng cách từ điểm $M$ đến đường tiệm cận ngang
Diện tích hình chữ nhật tạo bởi hai đường tiệm cận của đồ thị hàm số $y=\dfrac{2x+1}{x+3}$ và các trục tọa độ bằng bao nhiêu?
Đáp án: 6Lời giải: Đường tiệm cận đứng của đồ thị hàm số $x=-3$;
Đường tiệm cận ngang của đồ thị hàm số $y=2$
Đường tiệm cận ngang của đồ thị hàm số $y=2$
Diện tích hình chữ nhật tạo bởi hai đường tiệm cận của đồ thị hàm số $y=\dfrac{2x+1}{x+3}$ và các trục tọa độ bằng bao nhiêu?Đáp án: 6Lời giải: Đường tiệm cận đứng của đồ thị hàm số $x=-3$;Đường tiệm cận ngang của đồ thị hàm số $y=2$.Hai đường tiệm cận tạo với các trục tọa độ một hình chữ nhât có chiều dài bằng $3$, chiều rộng bằng $2$.Diện tích hình chữ nhật: $S=2.3=6$. … [Đọc thêm...] vềDiện tích hình chữ nhật tạo bởi hai đường tiệm cận của đồ thị hàm số $y=\dfrac{2x+1}{x+3}$ và các trục tọa độ bằng bao nhiêu?
Đáp án: 6
Lời giải: Đường tiệm cận đứng của đồ thị hàm số $x=-3$;
Đường tiệm cận ngang của đồ thị hàm số $y=2$
Cho đồ thị hai hàm số $f\left( x \right)=\dfrac{x+1}{x-1}$ và $g\left( x \right)=\dfrac{ax+1}{x-2}$, $a\ne -\dfrac{1}{2}$
Cho đồ thị hai hàm số $f\left( x \right)=\dfrac{x+1}{x-1}$ và $g\left( x \right)=\dfrac{ax+1}{x-2}$, $a\ne -\dfrac{1}{2}$. Tìm giá trị thực dương của $a$ để các tiệm cận của hai đồ thị hàm số tạo thành một hình chữ nhật có diện tích là $4$.Đáp án: 5Lời giải: Đồ thị hàm số $f\left( x \right)=\dfrac{x+1}{x-1}$ có hai đường tiệm cận là $x=1$ và $y=1$.Đồ thị hàm số $g\left( x … [Đọc thêm...] vềCho đồ thị hai hàm số $f\left( x \right)=\dfrac{x+1}{x-1}$ và $g\left( x \right)=\dfrac{ax+1}{x-2}$, $a\ne -\dfrac{1}{2}$
Cho hàm số $y=\dfrac{2x+2}{2x-3}$ có đồ thị $\left( C \right)$
Cho hàm số $y=\dfrac{2x+2}{2x-3}$ có đồ thị $\left( C \right)$. Có bao nhiêu điểm $M$ thuộc $\left( C \right)$ sao cho khoảng cách từ điểm $M$ đến đường tiệm cận ngang bằng $10$ lần khoảng cách từ điểm $M$ đến đường tiệm cận đứng.Đáp án: 2Lời giải: Ta có các đường thẳng $x=\dfrac{3}{2}$ và $y=1$ lần lượt là đường tiệm cận đứng và đường tiệm cận ngang của đồ thị hàm số mà $M\in … [Đọc thêm...] vềCho hàm số $y=\dfrac{2x+2}{2x-3}$ có đồ thị $\left( C \right)$
