Cho hàm số $y=f\left( x \right)$ có đồ thị như hình vẽ.

Bài toán gốc

Cho hàm số $y=f\left( x \right)$ có đồ thị như hình vẽ.

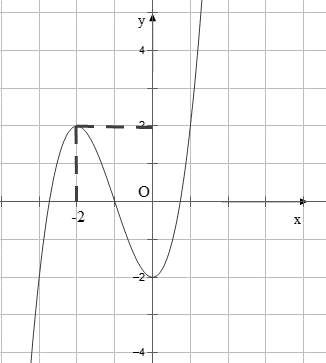
a) Đường thẳng $y=2$ là tiệm cận ngang của đồ thị $y=f\left( x \right)$.
.

b) $\lim\limits_{x\to \pm \infty }\dfrac{1}{f\left( x \right)-1}=1$.
.

c) Đồ thị $y=\dfrac{2019}{f\left( x \right)-1}$ có tiệm cận ngang là $y=0$.
.

d) Số tiệm cận đứng của đồ thị hàm số $y=\dfrac{2019}{f\left( x \right)-1}$ là 2.
.

Lời giải: 2
(Sai) Đường thẳng $y=2$ là tiệm cận ngang của đồ thị $y=f\left( x \right)$.

(Vì): Vì $\lim\limits_{x\to \pm \infty }f\left( x \right)=\pm \infty$ nên hàm số không có tiệm cận ngang.
(Sai) $\lim\limits_{x\to \pm \infty }\dfrac{1}{f\left( x \right)-1}=1$.

(Vì): Vì khi $x\to \pm \infty$ thì $f\left( x \right)\to \pm \infty$ nên $\lim\limits_{x\to \pm \infty }\dfrac{1}{f\left( x \right)-1}=0$.
(Đúng) Đồ thị $y=\dfrac{2019}{f\left( x \right)-1}$ có tiệm cận ngang là $y=0$.

(Vì): Vì $\lim\limits_{x\to \pm \infty }\dfrac{2019}{f\left( x \right)-1}=0$ (do $f\left( x \right)\to \pm \infty$ khi $x\to \pm \infty$) nên đồ thị $y=\dfrac{2019}{f\left( x \right)-1}$ có tiệm cận ngang là $y=0$.
(Sai) Số tiệm cận đứng của đồ thị hàm số $y=\dfrac{2019}{f\left( x \right)-1}$ là 2.

(Vì): Tập xác định của hàm số $y=f\left( x \right)$ là $D=\mathbb{R}$. Số đường tiệm cận đứng của đồ thị hàm số $y=\dfrac{2019}{f\left( x \right)-1}$ chính là số nghiệm của phương trình $f\left( x \right)-1=0 \Leftrightarrow f\left( x \right)=1$. Qua đồ thị ta có: Đường thẳng $y=1$ cắt đồ thị hàm số $y=f\left( x \right)$ tại 3 điểm phân biệt nên phương trình $f\left( x \right)=1$ có 3 nghiệm phân biệt. Vậy đồ thị hàm số $y=\dfrac{2019}{f\left( x \right)-1}$ có 3 đường tiệm cận đứng.

Phân tích và Phương pháp giải

Dạng bài tập này yêu cầu xác định các đường tiệm cận ngang (TCN) và tiệm cận đứng (TCĐ) của một hàm số phân thức $y = h(x)/g(x)$ dựa trên việc phân tích giới hạn và nghiệm của hàm số $f(x)$ được cho qua đồ thị.
1. TCN được xác định bằng cách tính $\lim_{x\to \pm \infty} g(x)$.
2. TCĐ được xác định bằng số nghiệm của phương trình mẫu số bằng 0 ($g(x)=0$), với điều kiện giới hạn của hàm số tại các nghiệm đó tiến tới vô cùng. Trong bài toán gốc, TCĐ của $y=\dfrac{C}{f(x)-a}$ chính là số nghiệm phân biệt của phương trình $f(x)=a$ không làm triệt tiêu tử số.

Bài toán tương tự

Cho hàm số $y=f\left( x \right)$ có đồ thị như hình vẽ bên dưới (mô tả bằng lời: Đồ thị hàm số có tiệm cận ngang là đường thẳng $y=-1$; đường thẳng $y=3$ cắt đồ thị $y=f(x)$ tại đúng 3 điểm phân biệt). Hỏi đồ thị hàm số $g\left( x \right)=\dfrac{50}{f\left( x \right)-3}$ có tổng cộng bao nhiêu đường tiệm cận?
A. 1
B. 2
C. 3
D. 4

Đáp án đúng: D. 4
Lời giải ngắn gọn:
1. Tiệm cận ngang (TCN): Do $\lim\limits_{x\to \pm \infty }f\left( x \right)=-1$, nên $\lim\limits_{x\to \pm \infty }g\left( x \right)=\lim\limits_{x\to \pm \infty }\dfrac{50}{f\left( x \right)-3}=\dfrac{50}{-1-3}=-\dfrac{50}{4}=-\dfrac{25}{2}$. Vậy đồ thị hàm số $g(x)$ có 1 TCN là $y=-25/2$.
2. Tiệm cận đứng (TCĐ): TCĐ là nghiệm của mẫu số $f\left( x \right)-3=0 \Leftrightarrow f\left( x \right)=3$. Theo giả thiết, phương trình $f(x)=3$ có 3 nghiệm phân biệt. Vậy đồ thị hàm số $g(x)$ có 3 TCĐ.
Tổng số tiệm cận là $1\text{ (TCN)} + 3\text{ (TCĐ)} = 4$.