Trắc nghiệm Tiệm cận

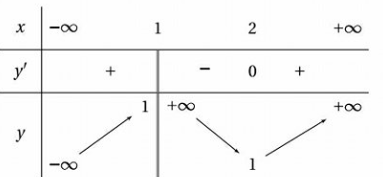
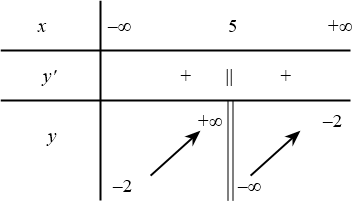
Bài toán gốc Cho hàm số $(C):y=f(x)=\dfrac{mx-1}{2x-4}$. Khi đóa) Nếu $m=-2$ thì đường thẳng $y=1$ là tiện cận ngang của $(C)$.b) Đồ thị hàm số đã cho có tiệm cận đứng khi $m\ne \dfrac{1}{2}$.c) Điểm $(2;3)$ là tâm đối xứng của đồ thị hàm số khi $m=6$.d) $\forall m\in \mathbb{R}$ ta có tiệm cận ngang của $(C)$ là đường thẳng $y=\dfrac{m}{2}$.Lời giải: Ta có TCĐ: $x=2$ … [Đọc thêm...] vềCho hàm số $(C):y=f(x)=\dfrac{mx-1}{2x-4}$. Khi đó

a) Nếu $m=-2$ thì đường thẳng $y=1$ là tiện cận ngang của $(C)$.

Bài toán gốc Nồng độ oxygen trong hồ theo thời gian $t$ cho bởi công thức $y\left( t \right)=5-\dfrac{15t}{9{{t}^{2}}+1}$, với $y$ được tính theo ${mg}/{l}\;$ và $t$ được tính theo giờ, $t\ge 0$.a) Đồ thị hàm số $y\left( t \right)$ có một đường tiệm cận ngang và một đường tiệm cận xiên.b) Đồ thị hàm số có đường tiệm cận ngang là $y=4$.c) Đồ thị … [Đọc thêm...] vềNồng độ oxygen trong hồ theo thời gian $t$ cho bởi công thức $y\left( t \right)=5-\dfrac{15t}{9{{t}^{2}}+1}$, với $y$ được tính theo ${mg}/{l}\;$ và $t$ được tính theo giờ, $t\ge 0$.

Bài toán gốc Cho hàm số $y=f\left( x \right)$ liên tục trên các khoảng xác định và có bảng biến thiên như hình vẽXét tính đúng sai của các mệnh đề sau:a) Đồ thị $\left( C \right)$ có đường tiệm cận đứng $x=1$.b) Đồ thị $\left( C \right)$ không có đường tiệm cận ngang.c) Đồ thị $\left( {{C}_{1}} \right):y=\dfrac{1}{f\left( x \right)}$ có không đường tiệm cận ngang.d) Số … [Đọc thêm...] vềCho hàm số $y=f\left( x \right)$ liên tục trên các khoảng xác định và có bảng biến thiên như hình vẽ

Bài toán gốc Xét tính đúng sai của các phát biểu sau:a) Đồ thị hàm số $y=\dfrac{-x+1}{4x+3}$ có tiệm cận đứng là đường thẳng $x=-\dfrac{1}{4}$.b) Đồ thị hàm số $y=\dfrac{-x+3}{-2x-2}$ có tiệm cận ngang là đường thẳng $y=\dfrac{1}{2}$.c) Đồ thị hàm số $y=\dfrac{x^2-2x-2}{x-2}$ có tiệm cận đứng đường thẳng $x=2$.d) Đồ thị hàm số $y=\dfrac{-x^2+5x+5}{x+1}$ có tiệm cận xiên … [Đọc thêm...] vềXét tính đúng sai của các phát biểu sau:

a) Đồ thị hàm số $y=\dfrac{-x+1}{4x+3}$ có tiệm cận đứng là đường thẳng $x=-\dfrac{1}{4}$.

Bài toán gốc Cho hàm số $y=f(x)$ có bảng biến thiên như hình dưới đây:Xét tính đúng sai của các phát biểu sau:a) Đồ thị hàm số $y=f(x)$ có tiệm cận đứng là đường thẳng $x=5$.b) Đồ thị hàm số $y=f(x)$ có tiệm cận đứng là đường thẳng $x=-5$.c) Đồ thị hàm số $y=f(x)$ có tiệm cận ngang là đường thẳng $y=-2$.d) Đồ thị hàm số $y=f(x)$ có tiệm cận ngang là đường thẳng … [Đọc thêm...] vềCho hàm số $y=f(x)$ có bảng biến thiên như hình dưới đây:

Bài toán gốc Xét tính đúng sai của các phát biểu sau:a) Đồ thị hàm số $y=x^3-2x^2-3x+1$ có tiệm cận.b) Đồ thị hàm số $y=\dfrac{-x-1}{3x+4}$ có tiệm cận.c) Đồ thị hàm số $y=\dfrac{x+4}{3x+12}$ không có tiệm cận đứng.d) Đồ thị hàm số $y=\dfrac{-x+3}{x+3}$ có tiệm cận đứng là đường thẳng $x=-3$, tiệm cận ngang là $y=-1$.Lời giải:(Sai) Đồ thị hàm số $y=x^3-2x^2-3x+1$ có … [Đọc thêm...] vềXét tính đúng sai của các phát biểu sau:

a) Đồ thị hàm số $y=x^3-2x^2-3x+1$ có tiệm cận.

Bài toán gốc Cho hàm số $y=f(x)$ xác định trên $\mathbb{R}\backslash \left\{ -2 \right\}$, liên tục trên mỗi khoảng xác định và có bảng biến thiên sau:Các mệnh đề sau đúng hay sai?a) Hàm số đạt cực đại tại điểm $x=-3$ và đạt cực tiểu tại $x=-1$.b) Đồ thị hàm số nhận đường thẳng $y=-2$ làm tiệm cận đứng.c) Hàm số nghịch biến trên khoảng $\left( -3;-1 \right)$.d) Đồ thị … [Đọc thêm...] vềCho hàm số $y=f(x)$ xác định trên $\mathbb{R}\backslash \left\{ -2 \right\}$, liên tục trên mỗi khoảng xác định và có bảng biến thiên sau:

Bài toán gốc Cho hàm số $y=f(x)=\dfrac{-x-3}{4x+2}$. Xét tính đúng sai của các phát biểu sau:a) Đồ thị hàm số $y=f(x)$ có tiệm cận đứng là đường thẳng $x=-\dfrac{1}{2}$.b) Đồ thị hàm số $y=f(x)$ có tiệm cận đứng là đường thẳng $x=\dfrac{1}{2}$.c) Đồ thị hàm số $y=f(x)$ có tiệm cận ngang là đường thẳng $y=-\dfrac{1}{4}$.d) Đồ thị hàm số $y=f(x)$ có tiệm cận ngang là … [Đọc thêm...] vềCho hàm số $y=f(x)=\dfrac{-x-3}{4x+2}$. Xét tính đúng sai của các phát biểu sau:

Bài toán gốc Cho hàm số $f\left( x \right)=\dfrac{{{x}^{2}}-2x+3}{x+2}$.a) Tập xác định của hàm số là $D=\mathbb{R}\backslash \left\{ -2 \right\}$.b) Hàm số có cực trị.c) Đồ thị hàm số cắt trục hoành.d) Đồ thị hàm số nhận điểm $I\left( -2;6 \right)$ làm tâm đối xứng.Lời giải: Đúng. Điều kiện xác định $x\ne -2$ nên tập xác định của hàm số là $D=\mathbb{R}\backslash … [Đọc thêm...] vềCho hàm số $f\left( x \right)=\dfrac{{{x}^{2}}-2x+3}{x+2}$.

Bài toán gốc Cho hàm số $y = \dfrac{-3x-3}{3x+2}$. Hãy xét tính đúng sai các khẳng định sau?a) Tập xác định của hàm số là $\mathscr{D} = \mathbb{R} \setminus \left\{{-\dfrac{2}{3}}\right\}$.b) Đạo hàm $y^{\prime} = \dfrac{-15}{(3x+2)^2}$.c) Hàm số nghịch biến trên các khoảng xác định của nó.d) Đường tiệm cận đứng và tiệm cận ngang của hàm số là $x = -\dfrac{2}{3}$ ; $y … [Đọc thêm...] vềCho hàm số $y = \dfrac{-3x-3}{3x+2}$. Hãy xét tính đúng sai các khẳng định sau?