Một tàu đổ bộ tiếp cận Mặt Trăng theo cách tiếp cận thẳng đứng và đốt cháy các tên lửa hãm ở độ cao $250$ km so với bề mặt của Mặt Trăng. Trong khoảng $50$ giây đầu tiên kể từ khi đốt cháy các tên lửa hãm, độ cao $h$ của con tàu so với bề mặt của Mặt Trăng được tính (gần đúng) bởi hàm $h\left( t \right)=-0,01{{t}^{3}}+1,1{{t}^{2}}-30t+250$ trong đó $t$ là thời gian tính bằng … [Đọc thêm...] vềMột tàu đổ bộ tiếp cận Mặt Trăng theo cách tiếp cận thẳng đứng và đốt cháy các tên lửa hãm ở độ cao $250$ km so với bề mặt của Mặt Trăng
Trắc nghiệm Giá trị lớn nhất và nhỏ nhất của hàm số
Cho một tấm nhôm hình vuông cạnh $2016\left( cm \right)$. Người ta cắt ở bốn góc của tấm nhôm đó bốn hình vuông bằng nhau, mỗi hình vuông có cạnh bằng $x\left( cm \right)$
Cho một tấm nhôm hình vuông cạnh $2016\left( cm \right)$. Người ta cắt ở bốn góc của tấm nhôm đó bốn hình vuông bằng nhau, mỗi hình vuông có cạnh bằng $x\left( cm \right)$, rồi gập tấm nhôm lại như hình vẽ dưới đây để được một cái hộp không nắp. Hỏi: a) Để hộp nhận được có thể tích lớn nhất thì $x=336\left( cm \right)$.b) Để hộp nhận được có thể tích lớn nhất thì $x=250\left( … [Đọc thêm...] vềCho một tấm nhôm hình vuông cạnh $2016\left( cm \right)$. Người ta cắt ở bốn góc của tấm nhôm đó bốn hình vuông bằng nhau, mỗi hình vuông có cạnh bằng $x\left( cm \right)$
Từ một tấm bìa hình chữ nhật có chiều rộng $10$ cm và chiều dài $60$ cm như hình a, người ta cắt ở bốn góc bốn hình vuông có cạnh $x$ với $2\le x\le 5$
Từ một tấm bìa hình chữ nhật có chiều rộng $10$ cm và chiều dài $60$ cm như hình a, người ta cắt ở bốn góc bốn hình vuông có cạnh $x$ với $2\le x\le 5$ và gấp lại để tạo thành chiếc hộp có dạng hình hộp chữ nhật không nắp như hình bên. Khi đó a) Mặt đáy của chiếc hộp có chiều rộng bằng $(10-x)$ và chiều dài bằng $(60-2x)$.b) Thể tích chiếc hộp là $V\left( x … [Đọc thêm...] vềTừ một tấm bìa hình chữ nhật có chiều rộng $10$ cm và chiều dài $60$ cm như hình a, người ta cắt ở bốn góc bốn hình vuông có cạnh $x$ với $2\le x\le 5$
Thể tích nước của một bể bơi sau t phút bơm tính theo công thức $V\left( t \right)=\dfrac{1}{100}\left( 30{{t}^{3}}-\dfrac{{{t}^{4}}}{4} \right)$, $\left( 0\le t\le 90 \right)$.
Thể tích nước của một bể bơi sau t phút bơm tính theo công thức $V\left( t \right)=\dfrac{1}{100}\left( 30{{t}^{3}}-\dfrac{{{t}^{4}}}{4} \right)$, $\left( 0\le t\le 90 \right)$. Tốc độ bơm nước tại thời điểm t được tính bởi $f\left( t \right)=V'\left( t \right)$. Trong các khẳng định sau, chọn khẳng định đúng hoặc sai?a) Tốc độ bơm tăng từ phút 0 đến phút thứ 75. … [Đọc thêm...] vềThể tích nước của một bể bơi sau t phút bơm tính theo công thức $V\left( t \right)=\dfrac{1}{100}\left( 30{{t}^{3}}-\dfrac{{{t}^{4}}}{4} \right)$, $\left( 0\le t\le 90 \right)$.
Một sợi dây kim loại dài $a$ $\left( \text{cm} \right)$. Người ta cắt đoạn dây đó thành hai đoạn có độ dài $x$ $\left( \text{cm} \right)$ được uốn thành đường tròn và đoạn còn lại được uốn thành hình vuông
Một sợi dây kim loại dài $a$ $\left( \text{cm} \right)$. Người ta cắt đoạn dây đó thành hai đoạn có độ dài $x$ $\left( \text{cm} \right)$ được uốn thành đường tròn và đoạn còn lại được uốn thành hình vuông $\left( a{>}x{>}0 \right).$ a) Bán kính đường tròn: $r=\dfrac{x}{\pi }$.b) Diện tích hình vuông: ${{\left( \dfrac{a-x}{2} \right)}^{2}}$.c) Tổng diện tích hai hình: … [Đọc thêm...] vềMột sợi dây kim loại dài $a$ $\left( \text{cm} \right)$. Người ta cắt đoạn dây đó thành hai đoạn có độ dài $x$ $\left( \text{cm} \right)$ được uốn thành đường tròn và đoạn còn lại được uốn thành hình vuông
Một vật chuyển động trên đường thẳng được xác định bởi công thức $s\left( t \right)={{t}^{3}}-3{{t}^{2}}+7t-2$, trong đó ${t{>}0}$ và tính bằng giây
Một vật chuyển động trên đường thẳng được xác định bởi công thức $s\left( t \right)={{t}^{3}}-3{{t}^{2}}+7t-2$, trong đó ${t{>}0}$ và tính bằng giây và ${s}$ là quãng đường chuyển động được của vật trong ${t}$ giây tính bằng mét. Khi đó:a) Thời điểm ${t=2}$ tại đó vận tốc của chuyển động đạt giá trị nhỏ nhất.b) Gia tốc của vật tại thời điểm mà vận tốc của chuyển động bằng … [Đọc thêm...] vềMột vật chuyển động trên đường thẳng được xác định bởi công thức $s\left( t \right)={{t}^{3}}-3{{t}^{2}}+7t-2$, trong đó ${t{>}0}$ và tính bằng giây
Cần rào ba cạnh để cùng với bờ tường có sẵn tạo thành mảnh vườn hình chữ nhật có diện tích $200{{\text{m}}^{2}}$. Kí hiệu $x\left( \text{ m} \right),y\left( \text{ m} \right)$ lần lượt là độ dài các cạnh của mảnh vườn vuông góc và song song với bờ tuờng
Cần rào ba cạnh để cùng với bờ tường có sẵn tạo thành mảnh vườn hình chữ nhật có diện tích $200{{\text{m}}^{2}}$. Kí hiệu $x\left( \text{ m} \right),y\left( \text{ m} \right)$ lần lượt là độ dài các cạnh của mảnh vườn vuông góc và song song với bờ tuờng; $L\left( \text{ m} \right)$ là tổng độ dài lưới thép cần để rào mảnh vườn. Biết rằng mỗi mét lưới thép dùng để rào mảnh vườn … [Đọc thêm...] vềCần rào ba cạnh để cùng với bờ tường có sẵn tạo thành mảnh vườn hình chữ nhật có diện tích $200{{\text{m}}^{2}}$. Kí hiệu $x\left( \text{ m} \right),y\left( \text{ m} \right)$ lần lượt là độ dài các cạnh của mảnh vườn vuông góc và song song với bờ tuờng
Cho một tấm nhôm hình vuông cạnh a. Người ta cắt ở 4 góc 4 hình vuông bằng nhau, rồi gập tấm nhôm lại để được một cái hộp không nắp.
Cho một tấm nhôm hình vuông cạnh a. Người ta cắt ở 4 góc 4 hình vuông bằng nhau, rồi gập tấm nhôm lại để được một cái hộp không nắp. a) Thể tích của khối hộp là lớn nhất khi cạnh của hình vuông bị cắt bằng $\dfrac{a}{12}$.b) Thể tích của khối hộp là lớn nhất khi cạnh của hình vuông bị cắt bằng $\dfrac{a}{12}$.c) Thể tích của khối hộp lớn nhất bằng $\dfrac{{{a}^{3}}}{27}.$.d) … [Đọc thêm...] vềCho một tấm nhôm hình vuông cạnh a. Người ta cắt ở 4 góc 4 hình vuông bằng nhau, rồi gập tấm nhôm lại để được một cái hộp không nắp.
Hàm số $y=f(x)$ có bảng biến trên $[-2;3]$ như hình dưới đây: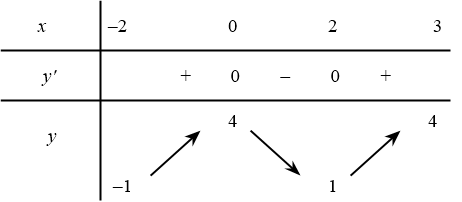
Xét tính đúng sai của các phát biểu sau:

Bài toán gốc Hàm số $y=f(x)$ có bảng biến trên $[-2;3]$ như hình dưới đây:Xét tính đúng sai của các phát biểu sau:a) Hàm số đồng biến trên $(0;3)$.b) Cực tiểu hàm số trên khoảng $(-2;3)$ bằng $2$.c) Hàm số đạt giá trị lớn nhất trên $[-2;3]$ tại điểm $x=3$.d) Hàm số đạt giá trị lớn nhất trên $[-2;3]$ tại điểm $x=2$.Lời giải: (Sai) Hàm số đồng biến trên $(0;3)$.(Sai) Cực … [Đọc thêm...] vềHàm số $y=f(x)$ có bảng biến trên $[-2;3]$ như hình dưới đây:

Xét tính đúng sai của các phát biểu sau:
Hàm số $y=2x^3-12x^2+18x+4$. Xét tính đúng sai của các phát biểu sau:a) Hàm số đồng biến trên $(3;+\infty)$
Bài toán gốc Hàm số $y=2x^3-12x^2+18x+4$. Xét tính đúng sai của các phát biểu sau:a) Hàm số đồng biến trên $(3;+\infty)$.b) Hàm số trên khoảng $(0;5)$ đạt cực tiểu tại điểm $x=1$.c) Giá trị lớn nhất của hàm số trên $[0;5]$ bằng $12$.d) Giá trị nhỏ nhất của hàm số trên $[0;5]$ bằng $4$.Lời giải: $y^{\prime}=6x^2-24x+18$$y^{\prime}=0\Leftrightarrow x_1=1,x_2=3$.(Đúng) Hàm … [Đọc thêm...] vềHàm số $y=2x^3-12x^2+18x+4$. Xét tính đúng sai của các phát biểu sau:
a) Hàm số đồng biến trên $(3;+\infty)$
