Từ một tấm bìa hình chữ nhật có chiều rộng $10$ cm và chiều dài $60$ cm như hình a, người ta cắt ở bốn góc bốn hình vuông có cạnh $x$ với $2\le x\le 5$

Từ một tấm bìa hình chữ nhật có chiều rộng $10$ cm và chiều dài $60$ cm như hình a, người ta cắt ở bốn góc bốn hình vuông có cạnh $x$ với $2\le x\le 5$ và gấp lại để tạo thành chiếc hộp có dạng hình hộp chữ nhật không nắp như hình bên. Khi đó

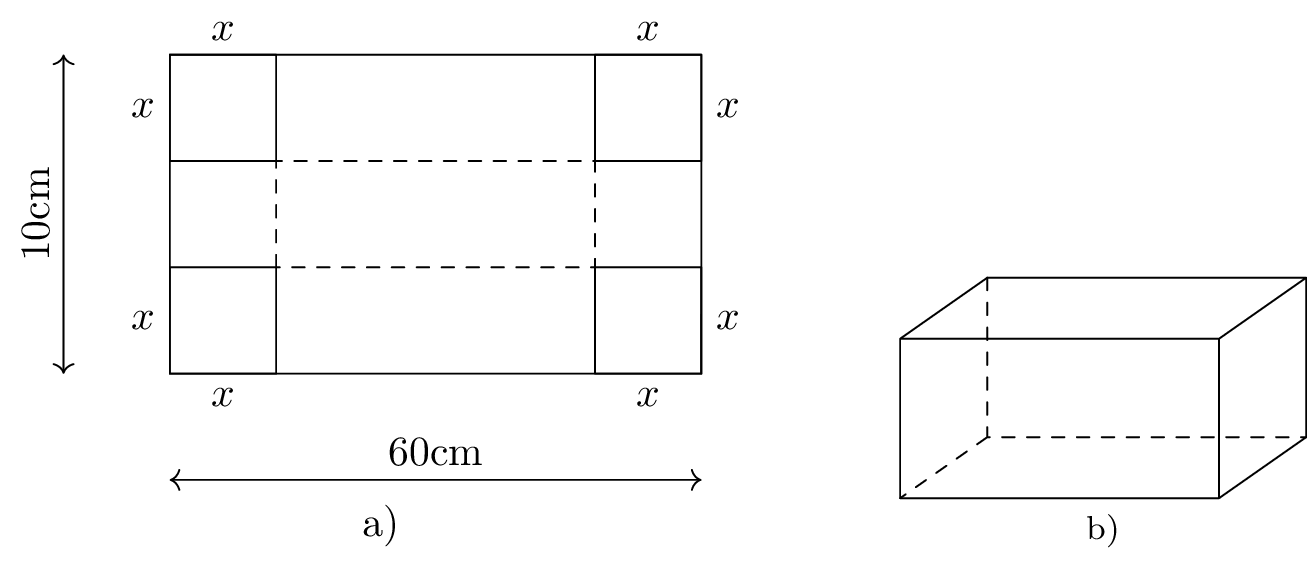
a) Mặt đáy của chiếc hộp có chiều rộng bằng $(10-x)$ và chiều dài bằng $(60-2x)$.

b) Thể tích chiếc hộp là $V\left( x \right)=4{{x}^{3}}-140{{x}^{2}}+600x$.

c) Thể tích hộp lớn nhất là $V\approx 688,9$ $c{{m}^{3}}$.

d) Tổng diện tích tấm bìa bị cắt bỏ là $22,8c{{m}^{2}}$.

Lời giải:
Chiều rộng đáy của chiếc hộp là $10-2x$ (cm).
Chiều dài đáy của chiếc hộp là $60-2x$ (cm).
Chiều cao của chiếc hộp là $x$ (cm).
Vì vậy, thể tích chiếc hộp là $V\left( x \right)=x\left( 10-2x \right)\left( 60-2x \right)=x\left( 4{{x}^{2}}-140x+600 \right)=4{{x}^{3}}-140{{x}^{2}}+600x$.
Miền xác định của $x$ là $2\le x\le 5$.
Để tìm thể tích lớn nhất, ta tính đạo hàm $V’\left( x \right)$:
$V’\left( x \right)=12{{x}^{2}}-280x+600$.
Đặt $V’\left( x \right)=0 \Rightarrow 12{{x}^{2}}-280x+600=0 \Rightarrow 3{{x}^{2}}-70x+150=0$.
Nghiệm của phương trình là $x=\dfrac{35-5\sqrt{31}}{3}$ và $x=\dfrac{35+5\sqrt{31}}{3}$.
Chỉ có $x=\dfrac{35-5\sqrt{31}}{3} \approx 2,388$ thuộc đoạn $[2; 5]$.
Ta tính giá trị của $V(x)$ tại các điểm mút và điểm cực trị trong đoạn:
$V(2) = 4(2)^3 – 140(2)^2 + 600(2) = 32 – 560 + 1200 = 672$ $c{{m}^{3}}$.
$V(5) = 4(5)^3 – 140(5)^2 + 600(5) = 500 – 3500 + 3000 = 0$ $c{{m}^{3}}$.
$V\left( \dfrac{35-5\sqrt{31}}{3} \right) \approx 688,9$ $c{{m}^{3}}$.
Vậy thể tích lớn nhất của chiếc hộp là $V_{\max} \approx 688,9$ $c{{m}^{3}}$, đạt được khi cạnh cắt $x = \dfrac{35-5\sqrt{31}}{3}$ (cm).
Tổng diện tích tấm bìa bị cắt bỏ là $4x^2$.
Với $x = \dfrac{35-5\sqrt{31}}{3}$, tổng diện tích bị cắt bỏ là $4 \times \left( \dfrac{35-5\sqrt{31}}{3} \right)^2 \approx 4 \times (2.388)^2 \approx 4 \times 5.7025 \approx 22,81$ $c{{m}^{2}}$.
(Sai) Mặt đáy của chiếc hộp có chiều rộng bằng $(10-x)$ và chiều dài bằng $(60-2x)$.
(Đúng) Thể tích chiếc hộp là $V\left( x \right)=4{{x}^{3}}-140{{x}^{2}}+600x$.
(Đúng) Thể tích hộp lớn nhất là $V\approx 688,9$ $c{{m}^{3}}$.
(Đúng) Tổng diện tích tấm bìa bị cắt bỏ là $22,8c{{m}^{2}}$.