Cần rào ba cạnh để cùng với bờ tường có sẵn tạo thành mảnh vườn hình chữ nhật có diện tích $200{{\text{m}}^{2}}$. Kí hiệu $x\left( \text{ m} \right),y\left( \text{ m} \right)$ lần lượt là độ dài các cạnh của mảnh vườn vuông góc và song song với bờ tuờng

Cần rào ba cạnh để cùng với bờ tường có sẵn tạo thành mảnh vườn hình chữ nhật có diện tích $200{{\text{m}}^{2}}$. Kí hiệu $x\left( \text{ m} \right),y\left( \text{ m} \right)$ lần lượt là độ dài các cạnh của mảnh vườn vuông góc và song song với bờ tuờng; $L\left( \text{ m} \right)$ là tổng độ dài lưới thép cần để rào mảnh vườn. Biết rằng mỗi mét lưới thép dùng để rào mảnh vườn có đơn giá 250 nghìn đồng.

a) $y$ được tính theo $x$ bằng công thức $y=\dfrac{200}{x}$.

b) $L$ được tính theo $x$ theo công thức $L=2x+\dfrac{200}{x}$.

c) $L$ đạt giá trị nhỏ nhất khi $x=20\left( \text{ m} \right)$.

d) Số tiền tối thiểu để mua lưới thép rào mảnh vườn là 2,5 triệu đồng.

Lời giải: Ta có $xy=200\Rightarrow y=\dfrac{200}{x}$.
$L=2x+y=2x+\dfrac{200}{x}$.
${L}’=2x-\dfrac{200}{{{x}^{2}}}=\dfrac{2\left( {{x}^{2}}-100 \right)}{{{x}^{2}}};{L}’=0\Leftrightarrow x=10$.
Bảng biến thiên:

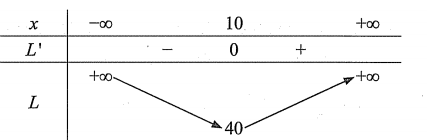
Giá trị nhỏ nhất của $L$ là 40 m khi $x=10\left( \text{ m} \right)$.
Số tiền tối thiểu để mua lưới thép rào mảnh vuờn là
$40\cdot 250=10000$ $=10$.
(Đúng) $y$ được tính theo $x$ bằng công thức $y=\dfrac{200}{x}$.
(Đúng) $L$ được tính theo $x$ theo công thức $L=2x+\dfrac{200}{x}$.
(Sai) $L$ đạt giá trị nhỏ nhất khi $x=20\left( \text{ m} \right)$.
(Sai) Số tiền tối thiểu để mua lưới thép rào mảnh vườn là 2,5 triệu đồng.