Sách Toán - Học toán

Giải bài tập Toán từ lớp 1 đến lớp 12, Học toán online và Đề thi toán

Trắc nghiệm Cực trị của hàm số

Cho hàm số bậc bốn trùng phương \(f\left( x \right)\) có bảng biến thiên như sau.

Ngày Thuộc chủ đề:Trắc nghiệm Cực trị của hàm số Tag với:,

Cho hàm số bậc bốn trùng phương \(f\left( x \right)\) có bảng biến thiên như sau. Số điểm cực trị của hàm số \(g\left( x \right) = \frac{1}{{{x^4}}}{\left[ {f\left( x \right) - 1} \right]^4}\) là A. \(6\) . B. \(5\). C. \(4\). D. \(7\). Lời giải Từ BBT của hàm số bậc bốn trùng phương \(f\left( x \right) = a{x^4} + b{x^2} + c\) ta thấy đồ thị hàm số nhận điểm có tọa độ … [Đọc thêm...] vềCho hàm số bậc bốn trùng phương \(f\left( x \right)\) có bảng biến thiên như sau.

Cho hàm số f(x) có f(0) = 0. Biết y = f'(x) là hàm số bậc bốn và có đồ thị như hình vẽ. Số điểm cực trị của hàm số \(g\left( x \right) = \left| {f\left( {{x^4}} \right) – {x^2}} \right|\)

Ngày Thuộc chủ đề:Trắc nghiệm Cực trị của hàm số Tag với:,

Câu hỏi: Cho hàm số f(x) có f(0) = 0. Biết y = f'(x) là hàm số bậc bốn và có đồ thị như hình vẽ. Số điểm cực trị của hàm số \(g\left( x \right) = \left| {f\left( {{x^4}} \right) - {x^2}} \right|\) là A. 4 B.3 C.6 D.5 ======== Đáp án đúng: D Xét hàm số \(h\left( x \right) = f\left( {{x^4}} \right) - {x^2}\) có \(h'\left( x \right) = … [Đọc thêm...] vềCho hàm số f(x) có f(0) = 0. Biết y = f'(x) là hàm số bậc bốn và có đồ thị như hình vẽ. Số điểm cực trị của hàm số \(g\left( x \right) = \left| {f\left( {{x^4}} \right) – {x^2}} \right|\)

Cho hàm số $f(x)=a x^{3}+b x^{2}+c x+1,(a \neq 0)$ với các số thực $a, b, c$ thoả mãn $a+b+c>2019$ và $\lim _{x \rightarrow+\infty} f(x)=-\infty .$ Số điềm cực trị của hàm số $y=|g(x-2019)|$ với $g(x)=f(x)-2020$ là

Ngày Thuộc chủ đề:Trắc nghiệm Cực trị của hàm số Tag với:

Cho hàm số $f(x)=a x^{3}+b x^{2}+c x+1,(a \neq 0)$ với các số thực $a, b, c$ thoả mãn $a+b+c>2019$ và $\lim _{x \rightarrow+\infty} f(x)=-\infty .$ Số điềm cực trị của hàm số $y=|g(x-2019)|$ với $g(x)=f(x)-2020$ làA. 4B. 2C. 5D. 3 Lời giải Chọn CTa có số điểm cực trị của hàm số $y=|g(x-2019)|$ bằng Số điểm cựa trị của hàm số$$y=|g(x)|$$Ta có $\lim _{x \rightarrow+\infty} … [Đọc thêm...] vềCho hàm số $f(x)=a x^{3}+b x^{2}+c x+1,(a \neq 0)$ với các số thực $a, b, c$ thoả mãn $a+b+c>2019$ và $\lim _{x \rightarrow+\infty} f(x)=-\infty .$ Số điềm cực trị của hàm số $y=|g(x-2019)|$ với $g(x)=f(x)-2020$ là

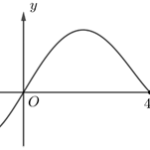
Câu 46: (MH Toan 2020) Cho hàm số bậc bốn \(y = f(x)\) có đồ thị như hình bên. Số điểm cực trị của hàm số \(g(x) = f\left( {{x^3} + 3{x^2}} \right)\) là

Ngày Thuộc chủ đề:Trắc nghiệm Cực trị của hàm số Tag với:

Câu 46: (MH Toan 2020) Cho hàm số bậc bốn \(y = f(x)\) có đồ thị như hình bên. Số điểm cực trị của hàm số \(g(x) = f\left( {{x^3} + 3{x^2}} \right)\) là A. \(5\). B. \(3\). C. \(7\). D. \(11\). Lời giải Đáp án: C Từ đồ thị, ta có bảng biến thiên của \(y = f(x)\) như sau: Ta có \(g(x) = f\left( {{x^3} + 3{x^2}} \right) \Rightarrow g\prime (x) = \left( {3{x^2} + 6x} … [Đọc thêm...] vềCâu 46: (MH Toan 2020) Cho hàm số bậc bốn \(y = f(x)\) có đồ thị như hình bên. Số điểm cực trị của hàm số \(g(x) = f\left( {{x^3} + 3{x^2}} \right)\) là

Đề: Tìm giá trị cực tiểu \({y_{CT}}\) của hàm số \(y = 2{x^3} + 3{x^2} – 12x + 2.\)

Ngày Thuộc chủ đề:Trắc nghiệm Cực trị của hàm số Tag với:

Câu hỏi: Tìm giá trị cực tiểu \({y_{CT}}\) của hàm số \(y = 2{x^3} + 3{x^2} - 12x + 2.\) A. \({y_{CT}} =  - 21\) B. \({y_{CT}} =  - 5\) C. \({y_{CT}} = 6\) D. \({y_{CT}} =  - 6\) Hãy chọn trả lời đúng trước khi xem đáp án và lời giải bên dưới. Có vấn đề về lời giải xin các bạn để … [Đọc thêm...] vềĐề: Tìm giá trị cực tiểu \({y_{CT}}\) của hàm số \(y = 2{x^3} + 3{x^2} – 12x + 2.\)

Đề: Cho đồ thị hàm số \(y = a{x^4} + b{x^3} + c\) đạt cực đại tại \(A\left( {0;3} \right)\) và cực tiểu \(B\left( { – 1;5} \right)\). Tính giá trị của \(P = a + 2b + 3c\)

Ngày Thuộc chủ đề:Trắc nghiệm Cực trị của hàm số Tag với:

Câu hỏi: Cho đồ thị hàm số \(y = a{x^4} + b{x^3} + c\) đạt cực đại tại \(A\left( {0;3} \right)\) và cực tiểu \(B\left( { - 1;5} \right)\). Tính giá trị của \(P = a + 2b + 3c\) A. \(P =  - 5\) B. \(P =  - 9\) C. \(P =  - 15\) D. \(P = 3\) Hãy chọn trả lời đúng trước khi xem đáp án … [Đọc thêm...] vềĐề: Cho đồ thị hàm số \(y = a{x^4} + b{x^3} + c\) đạt cực đại tại \(A\left( {0;3} \right)\) và cực tiểu \(B\left( { – 1;5} \right)\). Tính giá trị của \(P = a + 2b + 3c\)

Đề: Hàm số \(y = \frac{{{e^x}}}{{x + 1}}\) có bao nhiêu điểm cực trị?

Ngày Thuộc chủ đề:Trắc nghiệm Cực trị của hàm số Tag với:

Câu hỏi: Hàm số \(y = \frac{{{e^x}}}{{x + 1}}\) có bao nhiêu điểm cực trị? A. 3 B. 2 C. 1 D. 0 Hãy chọn trả lời đúng trước khi xem đáp án và lời giải bên dưới. Có vấn đề về lời giải xin các bạn để lại phản hồi cuối bài. Đáp án đúng: C Hàm số có tập xác định \(D = … [Đọc thêm...] vềĐề: Hàm số \(y = \frac{{{e^x}}}{{x + 1}}\) có bao nhiêu điểm cực trị?

Đề: Cho hàm số \(f\left( x \right)\) có đạo hàm trên khoảng \(\left( {a;b} \right)\) chứa điểm \({x_0}\) (có thể hàm số \(f\left( x \right)\) không có đạo hàm tại điểm \({x_0}\)). Trong các khẳng định sau đây, khẳng định nào đúng?

Ngày Thuộc chủ đề:Trắc nghiệm Cực trị của hàm số Tag với:

Câu hỏi: Cho hàm số \(f\left( x \right)\) có đạo hàm trên khoảng \(\left( {a;b} \right)\) chứa điểm \({x_0}\) (có thể hàm số \(f\left( x \right)\) không có đạo hàm tại điểm \({x_0}\)). Trong các khẳng định sau đây, khẳng định nào đúng? A. Nếu f(x) không có đạo hàm tại điểm \({x_0}\) thì \(f\left( x \right)\) không đạt cực … [Đọc thêm...] vềĐề: Cho hàm số \(f\left( x \right)\) có đạo hàm trên khoảng \(\left( {a;b} \right)\) chứa điểm \({x_0}\) (có thể hàm số \(f\left( x \right)\) không có đạo hàm tại điểm \({x_0}\)). Trong các khẳng định sau đây, khẳng định nào đúng?

Đề: Tìm nguyên hàm \(F\left( x \right)\) của hàm số \(f\left( x \right) = \left( {{x^2} – 1} \right){e^{{x^3} – 3{\rm{x}}}}\) biết rằng hàm số \(F\left( x \right)\) có điểm cực tiểu nằm trên trục hoành.

Ngày Thuộc chủ đề:Trắc nghiệm Cực trị của hàm số Tag với:

Câu hỏi: Tìm nguyên hàm \(F\left( x \right)\) của hàm số \(f\left( x \right) = \left( {{x^2} - 1} \right){e^{{x^3} - 3{\rm{x}}}}\) biết rằng hàm số \(F\left( x \right)\) có điểm cực tiểu nằm trên trục hoành. A. \(F\left( x \right) = {e^{{x^3} - 3{\rm{x}}}} - {e^2}.\) B. \(F\left( x \right) = \frac{{{e^{{x^3} - 3x + 2}} - 1}}{{3{e^2}}}.\) C. \(F\left( … [Đọc thêm...] vềĐề: Tìm nguyên hàm \(F\left( x \right)\) của hàm số \(f\left( x \right) = \left( {{x^2} – 1} \right){e^{{x^3} – 3{\rm{x}}}}\) biết rằng hàm số \(F\left( x \right)\) có điểm cực tiểu nằm trên trục hoành.

Đề: Cho hàm số \(y = \frac{{x + 1}}{{x – 1}}\). Khẳng định nào sau đây là đúng?

Ngày Thuộc chủ đề:Trắc nghiệm Cực trị của hàm số Tag với:

Câu hỏi: Cho hàm số \(y = \frac{{x + 1}}{{x - 1}}\). Khẳng định nào sau đây là đúng? A. Hàm số có một điểm cực đại. B. Hàm số có một điểm cực tiểu. C. Hàm số có một điểm cực đại và một cực tiểu. D. Không có cực trị. Hãy chọn trả lời đúng trước khi xem đáp án và lời giải bên dưới. … [Đọc thêm...] vềĐề: Cho hàm số \(y = \frac{{x + 1}}{{x – 1}}\). Khẳng định nào sau đây là đúng?