Thể tích nước của một bể bơi sau $t$ phút bơm được tính theo công thức $V(t) = \dfrac{240t^3 – 4t^4}{100}$ với $0 \leq t \leq 90$

Thể tích nước của một bể bơi sau $t$ phút bơm được tính theo công thức $V(t) = \dfrac{240t^3 – 4t^4}{100}$ với $0 \leq t \leq 90$. Tốc độ bơm nước ở thời điểm $t$ được tính theo công thức $v(t) = V'(t)$. Tìm tốc độ bơm nước là lớn nhất?
Đáp án: 2160

Lời giải: Ta có $v(t) = V'(t) = – \dfrac{4 t^{3}}{25} + \dfrac{36 t^{2}}{5}$. Ta khảo sát hàm số $v(t)$ để tìm thời điểm tốc độ bơm nước là lớn nhất.
Ta có $v'(t) = – \dfrac{12 t^{2}}{25} + \dfrac{72 t}{5}$; $v'(t) = 0$ ta được $t =0; t =30$.
Bảng biến thiên

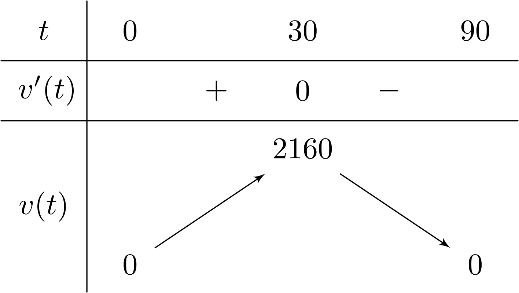
Từ bảng biến thiên ta thấy tốc độ bơm nước lớn nhất bằng 2160, tại thời điểm $t = 30$ phút.