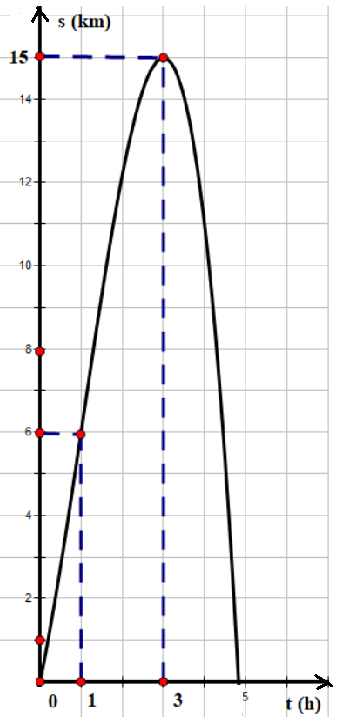
Thầy Lộc tham dự giải “Đi bộ trực tuyến Ngành Giáo dục và Đào tạo Edu Run-HCMC” năm 2024. Quãng đường thầy Lộc đi được biểu diễn bằng hàm số $s\left( t \right)=a{{t}^{3}}+b{{t}^{2}}+ct+d$ (với $a\ne 0$ ) có đồ thị như hình bên dưới (trong đó $t$ là thời gian tính bằng giờ, $s$ là quãng đường tính bằng km). Khi đó, vận tốc tối đa của thầy Lộc đạt được là bao nhiêu km/h? (làm tròn đến chữ số hàng phần mười)
Đáp án: 1,05
Lời giải: Dựa vào đồ thị ta thấy đồ thị hàm số đi qua các điểm: $O\left( 0;0 \right),A\left( 1;6 \right),B\left( 3;15 \right)$ và nhận $B\left( 3;15 \right)$ làm 1 điểm cực trị.
Ta có: $s\left( t \right)=a{{t}^{3}}+b{{t}^{2}}+ct+d\Rightarrow s’\left( t \right)=3a{{t}^{2}}+2bt+c$
Khi đó ta có hệ sau: $\left\{ \begin{array}{l} s\left( 0 \right)=0 \\ s\left( 1 \right)=6 \\ s\left( 3 \right)=15 \\ s’\left( 3 \right)=0 \end{array} \right.\Leftrightarrow \left\{ \begin{array}{l} d=0 \\ a+b+c+d=6 \\ 27a+9b+3c+d=15 \\ 27a+6b+c=0 \end{array} \right.\Leftrightarrow \left\{ \begin{array}{l} a=-7/12 \\ b=11/9 \\ c=19/4 \\ d=0 \end{array} \right.$
Nên: $s\left( t \right)=-\dfrac{7}{12}{{t}^{3}}+\dfrac{11}{6}{{t}^{2}}+\dfrac{19}{4}t$ $\Rightarrow v\left( t \right)=s’\left( t \right)=-\dfrac{7}{4}{{t}^{2}}+\dfrac{11}{3}t+\dfrac{19}{4}$.
Thầy Lộc dừng đi bộ khi: $v\left( t \right)=0\Leftrightarrow -\dfrac{7}{4}{{t}^{2}}+\dfrac{11}{3}t+\dfrac{19}{4}=0\Leftrightarrow \left[ \begin{array}{l} t=-\dfrac{19}{21} \\ t=3 \end{array} \right.$
Bài toán trở thành tìm giá trị lớn nhất của $v\left( t \right)$ trên $\left[ 0;3 \right]$.
Ta có: $v’\left( t \right)=-\dfrac{7}{2}t+\dfrac{11}{3}$ $\Rightarrow v’\left( t \right)=0\Leftrightarrow t=\dfrac{22}{21}$.
Khi đó: $v\left( 0 \right)=\dfrac{19}{4},v\left( 3 \right)=0,v\left( \dfrac{22}{21} \right)=\dfrac{1681}{252}\approx 6,67$
Vậy vận tốc lớn nhất mà thầy Lộc đạt được là 6,67 km/h tại thời điểm $t=\dfrac{22}{21}\left( h \right)\approx 1,05\left( h \right)$.
