Tại một nhà máy, khi sản xuất $x$ tạ sản phẩm ($x {>} 0$) mỗi ngày thì chi phí trung bình trên mỗi tạ sản phẩm được tính bởi công thức
$C(x) = x + 1 + \frac{9}{x} \text{ (triệu đồng/tạ)

Tại một nhà máy, khi sản xuất $x$ tạ sản phẩm ($x {>} 0$) mỗi ngày thì chi phí trung bình trên mỗi tạ sản phẩm được tính bởi công thức
$C(x) = x + 1 + \frac{9}{x} \text{ (triệu đồng/tạ).}$ Tính chi phí trung bình thấp nhất (tính theo triệu đồng/tạ) mà nhà máy có thể đạt được trong ngày.
Đáp án: 7

Lời giải: Ta có $C'(x) = 1 – \frac{9}{x^{2}}.$
Giải phương trình $C'(x) = 0$, ta được $x = 3$ (do $x {>} 0$).
Lập bảng biến thiên

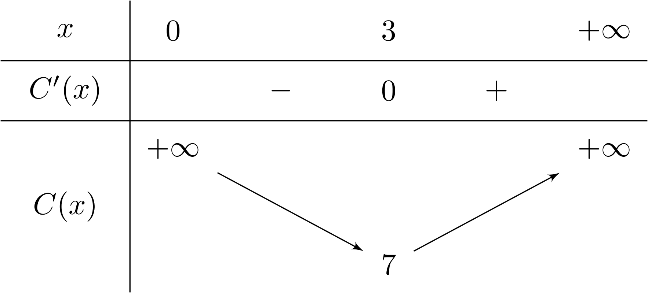
Từ đó, chi phí trung bình thấp nhất là $7$ triệu đồng/tạ.