Câu hỏi: Cho hình chóp\(\frac{{27}}{2}V\)có đáy\(\frac{9}{4}V\)là hình thoi cạnh \(a\),\(\widehat {BAD} = {60^\circ }\), tam giác\(SAD\)đều và nằm trong mặt phẳng vuông góc với đáy. Khoảng cách\(\frac{{SM}}{{ME}} = 2\)giữa hai đường thẳng\(SA\)và\(BD\)bằng A. \(\frac{{a\sqrt 6 }}{4}\). B. \(\frac{{a\sqrt 6 }}{2}\). C. \(\frac{{a\sqrt {15} }}{{10}}\). D. \(\frac{{a\sqrt {15} }}{5}\). LỜI GIẢI CHI TIẾT +) Gọilà trung […]
Trắc nghiệm tính khoảng cách HHKG
Cho lăng trụ đứng tam giác\(AB
C. A’B’C’\)có đáy là một tam giác vuông cân tại\(B\),\(AB = BC = a\),\(AA’ = a\sqrt 2 \),\(M\)là trung điểm\(BC\).Tính khoảng cách giữa hai đường thẳng\(AM\)và\(B’C\).
Câu hỏi: Cho lăng trụ đứng tam giác\(AB C. A’B’C’\)có đáy là một tam giác vuông cân tại\(B\),\(AB = BC = a\),\(AA’ = a\sqrt 2 \),\(M\)là trung điểm\(BC\).Tính khoảng cách giữa hai đường thẳng\(AM\)và\(B’C\). A. \(\frac{{a\sqrt 7 }}{7}\). B. \(\frac{{a\sqrt 3 }}{2}\). C. \(\frac{{2a}}{{\sqrt 5 }}\). D. \(a\sqrt 3 \). LỜI GIẢI CHI TIẾT +) […]
Cho hình hộp\(ABCD. A’B’C’D’\)cótất cả các cạnh đều bằng\(a\)và ba góc đỉnh\(A\)đều bằng\({60^\circ }\). Tính khoảng cách giữa hai đường thẳng\(AB\)và\(CC’\)
Câu hỏi: Cho hình hộp\(ABCD. A’B’C’D’\)cótất cả các cạnh đều bằng\(a\)và ba góc đỉnh\(A\)đều bằng\({60^\circ }\). Tính khoảng cách giữa hai đường thẳng\(AB\)và\(CC’\) A. \(\frac{{a\sqrt 6 }}{2}\). B. \(\frac{{a\sqrt 6 }}{3}\). C. \(\frac{{a\sqrt 6 }}{4}\). D. \(\frac{{a\sqrt 6 }}{6}\). LỜI GIẢI CHI TIẾT Hình hộp\(ABCD. A’B’C’D’\)cótất cả các cạnh đều bằng\(a\)và ba góc đỉnh\(A\)đều bằng\({60^\circ […]
Sử dụng khoảng cách để tính góc.
Cho hình chóp \(S.ABCD\) có đáy là hình thoi cạnh \(a\), góc \(\widehat {BAD} = 60^\circ \). Hình chiếu vuông góc của đỉnh \(S\) lên mặt phẳng \(\left( {ABCD} \right)\) là điểm \(H\) trên cạnh \(AB\) sao cho \(HA = 2HB\). Góc giữa \(SC\) và mặt phẳng \(\left( {ABCD} \right)\) bằng \(60^\circ \). Tính sin của góc giữa hai mặt phẳng \(\left( {SAC} \right)\) và \(\left( {SCD} \right)\).
Câu hỏi: Sử dụng khoảng cách để tính góc. Cho hình chóp \(S.ABCD\) có đáy là hình thoi cạnh \(a\), góc \(\widehat {BAD} = 60^\circ \). Hình chiếu vuông góc của đỉnh \(S\) lên mặt phẳng \(\left( {ABCD} \right)\) là điểm \(H\) trên cạnh \(AB\) sao cho \(HA = 2HB\). Góc giữa \(SC\) và mặt […]
Cho lăng trụ tam giác $A B C A^{\prime} B^{\prime} C^{\prime}$ có đáy $A B C$ là tam giác đều cạnh $a$. Hình chiếu vuông góc của $A^{\prime}$ trên mặt phẳng $(A B C)$ là trung điểm $O_{O}^{\top} \mathrm{c}^{\prime} \operatorname{anh} A B$. Góc giữa đường thẳng $A A^{\prime}$ và mặt phẳng $\left(A^{\prime} B^{\prime} C^{\prime}\right)$ là $60^{\circ} .$ Gọi $I$ là trung điểm cạnh $B^{\prime} C^{\prime}$. Khoảng cách từ $I$ đến đường thẳng $A^{\prime} C$ bằng
Câu hỏi: Cho lăng trụ tam giác $A B C A^{\prime} B^{\prime} C^{\prime}$ có đáy $A B C$ là tam giác đều cạnh $a$. Hình chiếu vuông góc của $A^{\prime}$ trên mặt phẳng $(A B C)$ là trung điểm $O_{O}^{\top} \mathrm{c}^{\prime} \operatorname{anh} A B$. Góc giữa đường thẳng $A A^{\prime}$ và mặt phẳng $\left(A^{\prime} B^{\prime} […]
Cho hình chóp tứ giác đềucó tất các các cạnhbằng. Khoảng cách từ điểm
đến mặt phẳng\(\left( {SBC} \right)\)bằng
đến mặt phẳng\(\left( {SBC} \right)\)bằngCâu hỏi: Cho hình chóp tứ giác đềucó tất các các cạnhbằng. Khoảng cách từ điểmđến mặt phẳng\(\left( {SBC} \right)\)bằng A. \(\frac{a \sqrt{6}}{3}\) B. \(\frac{a \sqrt{6}}{6}\) C. \(\frac{a \sqrt{2}}{2}\) D. \(\frac{a \sqrt{3}}{2}\) LỜI GIẢI CHI TIẾT Cách 1 Gọi\(O\)là tâm củahình vuông\(ABCD\). Dohình chóp \(S.ABCD\)là hình chóp tứ giác đều nên\(SO \bot (ABCD)\). Ta có […]
Cho hình chóp\(S.ABCD\)có đáy\(ABCD\)là hình thang vuông tại\(A\)và\(B\), \(AB = BC = a\),\(\Delta ABO\).\(SA\)vuông góc với mặt phẳng\(\left( {ABCD} \right)\), đường thẳng\(SC\)tạo với mặt phẳng\(\left( {SAB} \right)\)một góc \({30^0}\). Khoảng cách từ\(A\)đến mặt phẳng\(\left( {SCD} \right)\)bằng
Câu hỏi: Cho hình chóp\(S.ABCD\)có đáy\(ABCD\)là hình thang vuông tại\(A\)và\(B\), \(AB = BC = a\),\(\Delta ABO\).\(SA\)vuông góc với mặt phẳng\(\left( {ABCD} \right)\), đường thẳng\(SC\)tạo với mặt phẳng\(\left( {SAB} \right)\)một góc \({30^0}\). Khoảng cách từ\(A\)đến mặt phẳng\(\left( {SCD} \right)\)bằng A. \(AO = \sqrt {A{B^2} – B{O^2}}= \sqrt {{x^2} – {a^2}} \). B. \(\frac{a}{2}\). C. \(2a\). D. […]
Cho hình lăng trụ đều\(ABC. A’B’C’\)có thể tích\(V = \frac{{{a^3}\sqrt 3 }}{2}\), tam giác\(AB’C’\)có diện tích là\(\frac{{{a^2}\sqrt {19} }}{4}\). Gọi\(M\) là trung điểm của cạnh\(A{A^\prime }\). Khoảng cách từ điểm\(M\) đến mặt phẳng\(\left( {AB’C’} \right)\)bằng
Câu hỏi: Cho hình lăng trụ đều\(ABC. A’B’C’\)có thể tích\(V = \frac{{{a^3}\sqrt 3 }}{2}\), tam giác\(AB’C’\)có diện tích là\(\frac{{{a^2}\sqrt {19} }}{4}\). Gọi\(M\) là trung điểm của cạnh\(A{A^\prime }\). Khoảng cách từ điểm\(M\) đến mặt phẳng\(\left( {AB’C’} \right)\)bằng A. \(\frac{{2a\sqrt {57} }}{{19}}\). B. \(\frac{{a\sqrt {57} }}{{19}}\). C. \(\frac{{6a\sqrt {57} }}{{19}}\). D. \(\frac{{3a\sqrt {57} }}{{19}}\). LỜI GIẢI […]
Chuyên đề Khoảng cách hình học 11 ôn thi tốt nghiệp 2020
Chuyên đề Khoảng cách hình học 11 ôn thi tốt nghiệp 2020 – file word tương tự câu 40 ĐỀ TOÁN tham khảo Tốt Nghiệp NĂM 2020 lần 2 của bộ. ————- 5. Khoảng cách giữa hai đường thẳng chéo nhau + Đường thẳng cắt cả a, b và cùng vuông góc với a, […]
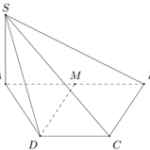
Câu 37: (MH Toan 2020) Cho hình chóp \(S.ABCD\) có đáy là hình thang, \(AB = 2a\), \(AD = DC = CB = a\), \(SA\) vuông góc với mặt phẳng đáy và \(SA = 3a\) (minh họa như hình bên). Gọi \(M\) là trung điểm của \(AB\). Khoảng cách giữa hai đường thẳng \(SB\) và \(DM\) bằng.
Câu 37: (MH Toan 2020) Cho hình chóp \(S.ABCD\) có đáy là hình thang, \(AB = 2a\), \(AD = DC = CB = a\), \(SA\) vuông góc với mặt phẳng đáy và \(SA = 3a\) (minh họa như hình bên). Gọi \(M\) là trung điểm của \(AB\). Khoảng cách giữa hai đường thẳng \(SB\) và […]