Câu hỏi: Cho hàm số \(y = \frac{{2x - 2}}{{x - 2}}\) có đồ thị là \(\left( C \right)\), \(M\)là điểm thuộc \(\left( C \right)\) sao cho tiếp tuyến của \(\left( C \right)\) tại \(M\)cắt hai đường tiệm cận của \(\left( C \right)\) tại hai điểm \(A\), \(B\) thỏa mãn \(AB = 2\sqrt 5 \). Gọi \(S\) là tổng các hoành độ của tất cả các điểm \(M\) thỏa mãn bài toán. Tìm giá trị của … [Đọc thêm...] vềCho hàm số \(y = \frac{{2x – 2}}{{x – 2}}\) có đồ thị là \(\left( C \right)\), \(M\)là điểm thuộc \(\left( C \right)\) sao cho tiếp tuyến của \(\left( C \right)\) tại \(M\)cắt hai đường tiệm cận của \(\left( C \right)\) tại hai điểm \(A\), \(B\) thỏa mãn \(AB = 2\sqrt 5 \). Gọi \(S\) là tổng các hoành độ của tất cả các điểm \(M\) thỏa mãn bài toán. Tìm giá trị của \(S\).
Trắc nghiệm tiệm cận vận dụng
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau

Tổng số đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số \(y = f\left( x \right)\)là
Câu hỏi: Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau Tổng số đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số \(y = f\left( x \right)\)là A. 1. B. 2. C. 3. D. 4. LỜI GIẢI CHI TIẾT Từ BBT ta thấy \(\mathop {\lim }\limits_{x \to - {1^ + }} f\left( x \right) = + \,\infty \) và\(\mathop {\lim }\limits_{x \to - {1^ - }} … [Đọc thêm...] vềCho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau
Tổng số đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số \(y = f\left( x \right)\)là
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\backslash \left\{ 1 \right\}\) và có bảng biến thiên như sau
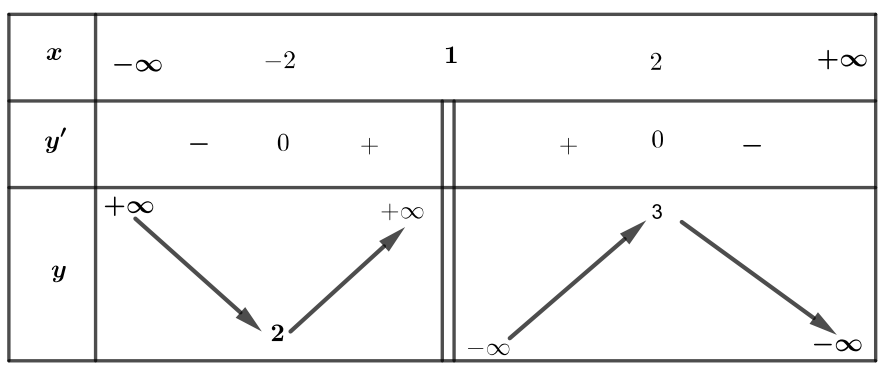
Đồ thị hàm số \(y = \frac{1}{{2f\left( x \right) – 5}}\) có bao nhiêu đường tiệm cận đứng?
Câu hỏi: Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\backslash \left\{ 1 \right\}\) và có bảng biến thiên như sau Đồ thị hàm số \(y = \frac{1}{{2f\left( x \right) - 5}}\) có bao nhiêu đường tiệm cận đứng? A. \(0\). B. \(4\). C. \(2\). D. \(1\). LỜI GIẢI CHI TIẾT Dựa vào BBT, phương trình \(2f\left( x \right) - 5 = 0\)\( … [Đọc thêm...] vềCho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\backslash \left\{ 1 \right\}\) và có bảng biến thiên như sau
Đồ thị hàm số \(y = \frac{1}{{2f\left( x \right) – 5}}\) có bao nhiêu đường tiệm cận đứng?
Cho hàm số \(y = \frac{{2x + 1}}{{x – 1}}\) có đồ thị là \(\left( C \right)\), \(I\) là giao điểm các đường tiệm cận của \(\left( C \right)\). Gọi \(M\) là điểm thuộc \(\left( C \right)\) sao cho tiếp tuyến của \(\left( C \right)\) tại \(M\) cắt hai đường tiệm cận tại \(A\) và \(B\) thỏa mãn chu vi tam giác \(IAB\) là nhỏ nhất. Khi đó có mấy điểm \(M\)thỏa mãn yêu cầu bài toán?
Câu hỏi: Cho hàm số \(y = \frac{{2x + 1}}{{x - 1}}\) có đồ thị là \(\left( C \right)\), \(I\) là giao điểm các đường tiệm cận của \(\left( C \right)\). Gọi \(M\) là điểm thuộc \(\left( C \right)\) sao cho tiếp tuyến của \(\left( C \right)\) tại \(M\) cắt hai đường tiệm cận tại \(A\) và \(B\) thỏa mãn chu vi tam giác \(IAB\) là nhỏ nhất. Khi đó có mấy điểm \(M\)thỏa mãn yêu … [Đọc thêm...] vềCho hàm số \(y = \frac{{2x + 1}}{{x – 1}}\) có đồ thị là \(\left( C \right)\), \(I\) là giao điểm các đường tiệm cận của \(\left( C \right)\). Gọi \(M\) là điểm thuộc \(\left( C \right)\) sao cho tiếp tuyến của \(\left( C \right)\) tại \(M\) cắt hai đường tiệm cận tại \(A\) và \(B\) thỏa mãn chu vi tam giác \(IAB\) là nhỏ nhất. Khi đó có mấy điểm \(M\)thỏa mãn yêu cầu bài toán?
Cho hàm số \(y = \frac{{2x + 1}}{{x + 1}}\) \(\left( C \right)\), gọi \(I\) là tâm đối xứng của đồ thị \(\left( C \right)\) và \(M\left( {a;b} \right)\) là một điểm thuộc đồ thị. Tiếp tuyến của đồ thị \(\left( C \right)\) tại điểm \(M\) cắt hai tiệm cận của đồ thị \(\left( C \right)\) lần lượt tại hai điểm \(A\) và \(B\). Để tam giác \(IAB\) có bán kính đường tròn nội tiếp lớn nhất thì tổng \(a + b\) bằng bao nhiêu?
Câu hỏi: Cho hàm số \(y = \frac{{2x + 1}}{{x + 1}}\) \(\left( C \right)\), gọi \(I\) là tâm đối xứng của đồ thị \(\left( C \right)\) và \(M\left( {a;b} \right)\) là một điểm thuộc đồ thị. Tiếp tuyến của đồ thị \(\left( C \right)\) tại điểm \(M\) cắt hai tiệm cận của đồ thị \(\left( C \right)\) lần lượt tại hai điểm \(A\) và \(B\). Để tam giác \(IAB\) có bán kính đường tròn … [Đọc thêm...] vềCho hàm số \(y = \frac{{2x + 1}}{{x + 1}}\) \(\left( C \right)\), gọi \(I\) là tâm đối xứng của đồ thị \(\left( C \right)\) và \(M\left( {a;b} \right)\) là một điểm thuộc đồ thị. Tiếp tuyến của đồ thị \(\left( C \right)\) tại điểm \(M\) cắt hai tiệm cận của đồ thị \(\left( C \right)\) lần lượt tại hai điểm \(A\) và \(B\). Để tam giác \(IAB\) có bán kính đường tròn nội tiếp lớn nhất thì tổng \(a + b\) bằng bao nhiêu?
Cho hàm số \(y = f\left( x \right)\) có đạo hàm liên tục trên \(\mathbb{R}\). Đồ thị hàm \(y = f\left( x \right)\) như hình vẽ. Hỏi đồ thị hàm số \(g\left( x \right) = \frac{{{x^2} – 1}}{{{f^2}\left( x \right) – 4f\left( x \right)}}\) có bao nhiêu đường tiệm cận đứng?

Câu hỏi: Cho hàm số \(y = f\left( x \right)\) có đạo hàm liên tục trên \(\mathbb{R}\). Đồ thị hàm \(y = f\left( x \right)\) như hình vẽ. Hỏi đồ thị hàm số \(g\left( x \right) = \frac{{{x^2} - 1}}{{{f^2}\left( x \right) - 4f\left( x \right)}}\) có bao nhiêu đường tiệm cận đứng? A. 4. B. 3. C. 1. D. 2. LỜI GIẢI CHI TIẾT Xét \({f^2}\left( x \right) - … [Đọc thêm...] vềCho hàm số \(y = f\left( x \right)\) có đạo hàm liên tục trên \(\mathbb{R}\). Đồ thị hàm \(y = f\left( x \right)\) như hình vẽ. Hỏi đồ thị hàm số \(g\left( x \right) = \frac{{{x^2} – 1}}{{{f^2}\left( x \right) – 4f\left( x \right)}}\) có bao nhiêu đường tiệm cận đứng?
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như hình vẽ bên.
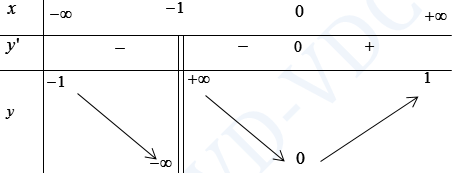
Khẳng định nào sau đây đúng?
Câu hỏi: Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như hình vẽ bên. Khẳng định nào sau đây đúng? A. Đồ thị hàm số có 3 đường tiệm cận. B. Đồ thị hàm số không có tiệm cận. C. Hàm số có giá trị lớn nhất bằng 1 và có giá trị nhỏ nhất bằng 0. D. Hàm số nghịch biến trên các khoảng\(\left( { - \infty ;0} \right)\) và \(\left( {0; + \infty } … [Đọc thêm...] vềCho hàm số \(y = f\left( x \right)\) có bảng biến thiên như hình vẽ bên.
Khẳng định nào sau đây đúng?
Cho hàm số \(y = \frac{{x + 2}}{{x – 2}}\) có đồ thị \(\left( C \right)\). Gọi \(I\) là giao điểm hai đường tiệm cận của \(\left( C \right)\). Tiếp tuyến của \(\left( C \right)\) cắt hai đường tiệm cận của \(\left( C \right)\) tại hai điểm \(A\), \(B\). Giá trị nhỏ nhất của chu vi đường tròn ngoại tiếp tam giác \(IAB\) bằng
Câu hỏi: Cho hàm số \(y = \frac{{x + 2}}{{x - 2}}\) có đồ thị \(\left( C \right)\). Gọi \(I\) là giao điểm hai đường tiệm cận của \(\left( C \right)\). Tiếp tuyến của \(\left( C \right)\) cắt hai đường tiệm cận của \(\left( C \right)\) tại hai điểm \(A\), \(B\). Giá trị nhỏ nhất của chu vi đường tròn ngoại tiếp tam giác \(IAB\) bằng A. \(4\sqrt 2 \pi \). B. \(8\pi … [Đọc thêm...] vềCho hàm số \(y = \frac{{x + 2}}{{x – 2}}\) có đồ thị \(\left( C \right)\). Gọi \(I\) là giao điểm hai đường tiệm cận của \(\left( C \right)\). Tiếp tuyến của \(\left( C \right)\) cắt hai đường tiệm cận của \(\left( C \right)\) tại hai điểm \(A\), \(B\). Giá trị nhỏ nhất của chu vi đường tròn ngoại tiếp tam giác \(IAB\) bằng
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ. Đồ thị hàm số đã cho có bao nhiêu đường tiệm cận.

Câu hỏi: Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ. Đồ thị hàm số đã cho có bao nhiêu đường tiệm cận. A. \(4\). B. \(2\). C. \(1\). D. \(3\). LỜI GIẢI CHI TIẾT Từ đồ thị hàm số ta thấy: Đồ thị hàm số có hai tiệm cận ngang là \(y = \pm 1\), hai tiệm cận đứng là \(x = \pm 2\). Vậy đồ thị hàm số có 4 đường tiệm cận. ======= Thuộc … [Đọc thêm...] vềCho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ. Đồ thị hàm số đã cho có bao nhiêu đường tiệm cận.
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau

Tổng số đường tiệm cận ngang và đường tiệm cận đứng của đồ thị hàm số đã cho là
Câu hỏi: Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau Tổng số đường tiệm cận ngang và đường tiệm cận đứng của đồ thị hàm số đã cho là A. \(4\) B. \(1\) C. \(3\) D. \(2\) LỜI GIẢI CHI TIẾT Từ bảng biến thiên ta có: \(\mathop {\lim }\limits_{x \to {1^ - }} y = + \infty \) nên đường thẳng \(x = 1\) là đường tiệm cận đứng của đồ thị … [Đọc thêm...] vềCho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau
Tổng số đường tiệm cận ngang và đường tiệm cận đứng của đồ thị hàm số đã cho là
