Khoảng cách trong không gian

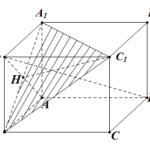
Đề bài: Cho hình lập phương $ABCD.A_1B_1C_1D_1$ cạnh $a$. Tìm khoảng cách giữa hai đường thẳng $A_1B;  B_1D$. Lời giải Ta có: $A_1B\bot B_1A (BAA_1B_1$ là hình vuông ); $A_1B \bot AD $( vì $AD \bot (BAA_1B_1)$)$\Rightarrow A_1B \bot (B_1AD) \Rightarrow A_1B\bot B_1D  (1)$Vì $DD_1 \bot (A_1B_1C_1D_1) \Rightarrow DD_1 \bot A_1C_1$.Do $A_1B_1C_1D_1$ là hình vuông nên … [Đọc thêm...] vềĐề bài: Cho hình lập phương $ABCD.A_1B_1C_1D_1$ cạnh $a$. Tìm khoảng cách giữa hai đường thẳng $A_1B;  B_1D$.

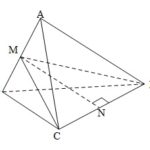
Đề bài: Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác vuông tại $B, AB=a, BC=2a$, cạnh $SA$ vuông góc với đáy và $SA=2a$. Xác định và tính độ dài đường vuông góc chung của hai đường thẳng $AB,SC$. Lời giải Gọi $M,N$ lần lượt là trung điểm của $SC,AB$.ta có: $MA=MB=\frac{SC}{2}\Rightarrow MN \bot AB$.Dễ thấy tam giác vuông $SAN$ bằng tam giác vuông $NBC\Rightarrow … [Đọc thêm...] vềĐề bài: Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác vuông tại $B, AB=a, BC=2a$, cạnh $SA$ vuông góc với đáy và $SA=2a$. Xác định và tính độ dài đường vuông góc chung của hai đường thẳng $AB,SC$.

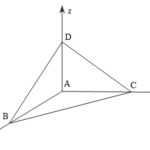
Đề bài: Cho tứ diện $ABCD$ có $AD\bot mp(ABC), AC=AD=4cm, AB=3cm, BC=5cm$. Tính khoảng cách từ $A$ đến $mp(BCD)$ Lời giải $\Delta ABC$ vuông tại $A$ vì $BC^2=25=AB^2+AC^2$Gắn hệ trục tọa độ như hình vẽ thì $A(0;0;0),, B(3;0;0), C(0;4;0), D(0;0;4)$Phương trình mặt chắn $(BCD):\frac{x}{3}+\frac{y}{4}+\frac{z}{4}=1\Leftrightarrow  4x+3y+3z-12=0  $Vậy: … [Đọc thêm...] vềĐề bài: Cho tứ diện $ABCD$ có $AD\bot mp(ABC), AC=AD=4cm, AB=3cm, BC=5cm$. Tính khoảng cách từ $A$ đến $mp(BCD)$

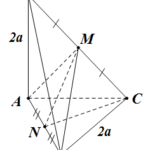
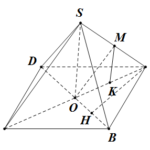
Đề bài: Cho hình chóp tứ giác đều $S.ABCD$, cạnh đáy bằng $a$. Gọi $E$ là điểm đối xứng của $D$ qua trung điểm của $SA$. Gọi $M,N$ tương ứng là trung điểm của $AE, BC$. Tìm khoảng cách theo $a$ giữa hai đường thẳng $MN,AC$. Lời giải Goi $P$ là trung điểm của $AB$ khi đó $MP//EB  (1)$Ta có: $SE// DA; SE=DA\Rightarrow SE//BC; SE=BC$$\Rightarrow SEBC $là hình binh hành … [Đọc thêm...] vềĐề bài: Cho hình chóp tứ giác đều $S.ABCD$, cạnh đáy bằng $a$. Gọi $E$ là điểm đối xứng của $D$ qua trung điểm của $SA$. Gọi $M,N$ tương ứng là trung điểm của $AE, BC$. Tìm khoảng cách theo $a$ giữa hai đường thẳng $MN,AC$.

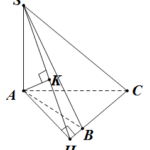
Đề bài: Cho hình chóp $S.ABC$ có $SA=3a$ và $SA$ vuông góc với mặt phẳng $(ABC)$. Giả sử $AB=BC=2a; \widehat{ABC}=120^0$ tìm khoảng cách từ $A$ đến mặt phẳng $(SBC)$. Lời giải Kẻ $AH \bot BC \Rightarrow SH \bot BC$ (định lí ba đường vuông góc).Lại có: $BC \bot (SAH)\Rightarrow (SBC)\bot (SAH)$.Do $(SBC) \cap (SAH)=AH,$nên nếu kẻ $AK \bot SH( K \in SH) \Rightarrow AK … [Đọc thêm...] vềĐề bài: Cho hình chóp $S.ABC$ có $SA=3a$ và $SA$ vuông góc với mặt phẳng $(ABC)$. Giả sử $AB=BC=2a; \widehat{ABC}=120^0$ tìm khoảng cách từ $A$ đến mặt phẳng $(SBC)$.

Đề bài: Cho hình chóp $S.ABCD$ đáy là hình thoi cạnh $AB=\sqrt{5}$, đường chéo $AC=4, SO=2\sqrt{2}$; và $SO$ vuông góc với mặt đáy $(ABCD)$, ở đây, $O$ là giao điểm của $AC,BD$. Gọi $M$ là trung điểm của cạnh $SC$. Tìm khoảng cách giữa hai đường thẳng $SA,BM$. Lời giải Ta có: $MO//SA\Rightarrow SA \bot (OMB)$$\Rightarrow d(SA,BM)=d(SA,(MOB))=d(S,(MOB))=d(C,(MOB)) … [Đọc thêm...] vềĐề bài: Cho hình chóp $S.ABCD$ đáy là hình thoi cạnh $AB=\sqrt{5}$, đường chéo $AC=4, SO=2\sqrt{2}$; và $SO$ vuông góc với mặt đáy $(ABCD)$, ở đây, $O$ là giao điểm của $AC,BD$. Gọi $M$ là trung điểm của cạnh $SC$. Tìm khoảng cách giữa hai đường thẳng $SA,BM$.

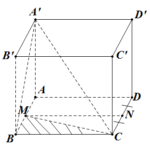
Đề bài: Cho hình lập phương $ABCD.A'B'C'D'$ có cạnh bằng $1$. Gọi $M,N$ lần lượt là trung điểm của $AB,CD$. Tính khoảng cách giữa hai đường thẳng $A'C, MN$ Lời giải Ta có $MN// BC\Rightarrow MN// (A'BC)$  $\Rightarrow d(MN, A'C)=d(MN, (A'BC))=D(M,(A'BC))  (1)$Dễ thấy … [Đọc thêm...] vềĐề bài: Cho hình lập phương $ABCD.A'B'C'D'$ có cạnh bằng $1$. Gọi $M,N$ lần lượt là trung điểm của $AB,CD$. Tính khoảng cách giữa hai đường thẳng $A'C, MN$

Đề bài: Cho hai mặt phẳng $(P)$ và $(Q)$ vuông góc với nhau, gọi $d$ là giao tuyến của chúng. Cho $2$ điểm $A\in (Q), B\in (P)$ thỏa mãn khoảng cách từ $B$ đến $(Q)$ bằng khoảng cách từ $A$ đến $(P)$. Chứng minh góc tạo bởi $AB$ với mặt phẳng $(P)$ và mặt phẳng $(Q)$ bằng nhau. Lời giải Ta có:Từ $A, B$ theo thứ tự kẻ $AA', BB'$ vuông góc với $d$. Do $P$ vuông góc … [Đọc thêm...] vềĐề bài: Cho hai mặt phẳng $(P)$ và $(Q)$ vuông góc với nhau, gọi $d$ là giao tuyến của chúng. Cho $2$ điểm $A\in (Q), B\in (P)$ thỏa mãn khoảng cách từ $B$ đến $(Q)$ bằng khoảng cách từ $A$ đến $(P)$. Chứng minh góc tạo bởi $AB$ với mặt phẳng $(P)$ và mặt phẳng $(Q)$ bằng nhau.

Đề bài: Cho tứ diện đều $ABCD$ cạnh $a$. Gọi $M, N$ theo thứ tự là trung điểm các cạnh $AB, CD$. Tìm độ dài đoạn $MN$ Lời giải Vì $ABCD$ là tứ diện đều cạnh $a$ nên các đường trung tuyến $CM=DM=\frac{a\sqrt{3}}{2}\Rightarrow \Delta CMD$ là tam giác cân đỉnh $M\Rightarrow MN$ vuông góc với $CD$.  Áp dụng định lý Pitago vào tam giác vuông $MND$ Ta … [Đọc thêm...] vềĐề bài: Cho tứ diện đều $ABCD$ cạnh $a$. Gọi $M, N$ theo thứ tự là trung điểm các cạnh $AB, CD$. Tìm độ dài đoạn $MN$

Đề bài: Cho tam giác $ABC$. Mặt phẳng song song với đường thẳng $BC$ cắt cạnh $AB$ tại $P$ và $AC$ tại $Q$. Điểm $P$ chia cạnh $AB$ theo tỉ số $3:5$ (bắt đầu từ điểm $A$). Tính độ dài đoạn $PQ$ nếu $BC=12cm$. Lời giải   Giả sử có mặt phẳng $\alpha$ song song với cạnh $BC$ và cắt mp $(ABC)$ theo giao tuyến $PQ$ thì $PQ//BC; \frac{PA}{PB}=\frac{3}{5}$ … [Đọc thêm...] vềĐề bài: Cho tam giác $ABC$. Mặt phẳng song song với đường thẳng $BC$ cắt cạnh $AB$ tại $P$ và $AC$ tại $Q$. Điểm $P$ chia cạnh $AB$ theo tỉ số $3:5$ (bắt đầu từ điểm $A$). Tính độ dài đoạn $PQ$ nếu $BC=12cm$.