Sự tăng trưởng của một loại virut được xác định bởi hàm số $p\left( t \right)=\dfrac{800}{1+7{{\text{e}}^{-0,2t}}}$, trong đó $t$ là thời gian được tính theo ngày

Sự tăng trưởng của một loại virut được xác định bởi hàm số $p\left( t \right)=\dfrac{800}{1+7{{\text{e}}^{-0,2t}}}$, trong đó $t$ là thời gian được tính theo ngày. Ở ngày thứ bao nhiêu thì tốc độ tăng trưởng của loài virut trên là lớn nhất?
Đáp án: 10

Lời giải: Tốc độ tăng trưởng của virut được tính theo hàm số $y={p}’\left( t \right)=\dfrac{1120.{{\text{e}}^{0,2t}}}{{{\left( {{\text{e}}^{0,2t}}+7 \right)}^{2}}}$, $t\ge 0$.
Xét hàm số $y=g\left( t \right)=\dfrac{1120.{{\text{e}}^{0,2t}}}{{{\left( {{\text{e}}^{0,2t}}+7 \right)}^{2}}}$, có ${g}’\left( t \right)=\dfrac{224.{{\text{e}}^{0,2t}}\left( 7-{{\text{e}}^{0,2t}} \right)}{{{\left( {{\text{e}}^{0,2t}}+7 \right)}^{3}}}$.
${g}’\left( t \right)=0\Leftrightarrow 7-{{e}^{0,2t}}=0\Leftrightarrow t=5\ln 7\approx 9,7$.
Ta có bảng dấu của ${g}’\left( t \right)$ như sau:

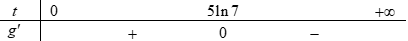
Dựa vào bảng trên ta thấy tốc độ tăng trưởng của virut sẽ đạt lớn nhất ở ngày thứ 10.