Sách Toán - Học toán

Giải bài tập Toán từ lớp 1 đến lớp 12, Học toán online và Đề thi toán

Kết quả tìm kiếm cho: ty so

Bài: Bảng số liệu thống kê – SGK Cánh Diều

Ngày Thuộc chủ đề:Giải bài tập Toán 3 - Cánh diều Tag với:

Giải bài tập thực hành Bài: Bảng số liệu thống kê ============ Chuyên mục: Giải bài tập Toán 3 - Cánh diều ============= Bài tập 1. Trang 95 sgk toán 3 tập 2 a) Quan sát bảng số liệu thống kê: b) Đọc bảng cho trong câu a và trả lời các câu hỏi: Cửa hàng đã nhập về bao nhiêu thùng kem dâu? Thùng kem loại nào được cửa hàng nhập về nhiều nhất? Thùng kem loại nào được … [Đọc thêm...] vềBài: Bảng số liệu thống kê – SGK Cánh Diều

Bài: Ôn tập về số và phép tính trong phạm vi 100 000 – SGK Cánh Diều

Ngày Thuộc chủ đề:Giải bài tập Toán 3 - Cánh diều Tag với:

Giải bài tập thực hành Bài: Ôn tập về số và phép tính trong phạm vi 100 000 ============ Chuyên mục: Giải bài tập Toán 3 - Cánh diều ============= Bài tập 1. Trang 105 sgk toán 3 tập 2 Điền >, <, =  Lời giải:   Bài tập 2. Trang 105 sgk toán 3 tập 2 Sắp xếp các số 4 768, 5 189, 4 827, 5 786 theo thứ tự: a) Từ bé đến lớn. b) Từ lớn đến bé. Lời giải: a) Sắp … [Đọc thêm...] vềBài: Ôn tập về số và phép tính trong phạm vi 100 000 – SGK Cánh Diều

Bài: Ôn tập về số và phép tính trong phạm vi 100 000 (tiếp theo) – SGK Cánh Diều

Ngày Thuộc chủ đề:Giải bài tập Toán 3 - Cánh diều Tag với:

Giải bài tập thực hành Bài: Ôn tập về số và phép tính trong phạm vi 100 000 (tiếp theo) ============ Chuyên mục: Giải bài tập Toán 3 - Cánh diều ============= Bài tập 1. Trang 107 sgk toán 3 tập 2 Tính nhẩm: 50 000 + 30 000                                30 000 x 2 70 000 – 50 000                                13 000 x 3 16 000 + 50 000                               … [Đọc thêm...] vềBài: Ôn tập về số và phép tính trong phạm vi 100 000 (tiếp theo) – SGK Cánh Diều

Bài: Ôn tập về một số yếu tố thống kê và xác suất – SGK Cánh Diều

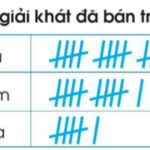
Ngày Thuộc chủ đề:Giải bài tập Toán 3 - Cánh diều Tag với:

Giải bài tập thực hành Bài: Ôn tập về một số yếu tố thống kê và xác suất ============ Chuyên mục: Giải bài tập Toán 3 - Cánh diều ============= Bài tập 1. Trang 111 sgk toán 3 tập 2 Một cửa hàng kiểm đếm mội số loại đồ uống giải khát đã bán trong ngày (tính theo cốc): Quan sát bảng ghi chép trên và trả lời các câu hỏi: Cửa hàng đã bán được bao nhiêu cốc nước mía? Đồ … [Đọc thêm...] vềBài: Ôn tập về một số yếu tố thống kê và xác suất – SGK Cánh Diều

Ông Bảo làm mái vòm ở phía trước ngôi nhà của mình bằng vật liệu tôn. Mái vòm đó là một phần của mặt xung quanh của một hình trụ như hình bên dưới. Biết giá tiền của 1\({m^2}\) tôn là \(300.000\) đồng. Hỏi số tiền (làm tròn đến hàng nghìn) mà ông Bảo mua tôn là bao nhiêu ?

Ngày Thuộc chủ đề:Trắc nghiệm Khối tròn xoay Tag với:,

Câu hỏi: Ông Bảo làm mái vòm ở phía trước ngôi nhà của mình bằng vật liệu tôn. Mái vòm đó là một phần của mặt xung quanh của một hình trụ như hình bên dưới. Biết giá tiền của 1\({m^2}\) tôn là \(300.000\) đồng. Hỏi số tiền (làm tròn đến hàng nghìn) mà ông Bảo mua tôn là bao nhiêu ? A. \(18.850.000\) đồng. B. \(5.441.000\) đồng. C. \(9.425.000\) đồng. … [Đọc thêm...] vềÔng Bảo làm mái vòm ở phía trước ngôi nhà của mình bằng vật liệu tôn. Mái vòm đó là một phần của mặt xung quanh của một hình trụ như hình bên dưới. Biết giá tiền của 1\({m^2}\) tôn là \(300.000\) đồng. Hỏi số tiền (làm tròn đến hàng nghìn) mà ông Bảo mua tôn là bao nhiêu ?

(Chuyên Lê Quý Đôn – Điện Biên – 2022) Trong không gian với hệ trục tọa độ \(Oxyz\), cho điểm \(A\left( {a;b;c} \right)\) với \(a;b;c\) là các số thực dương thỏa mãn \(5\left( {{a^2} + {b^2} + {c^2}} \right) = 9\left( {ab + 2bc + ca} \right)\) và \(Q = \frac{a}{{{b^2} + {c^2}}} – \frac{1}{{{{\left( {a + b + c} \right)}^3}}}\) có giá trị lớn nhất. Gọi \(M,N,P\) lần lượt là hình chiếu vuông góc của \(A\) lên các tia \(Ox,Oy,Oz\). Phương trình mặt phẳng \(\left( {MNP} \right)\) là

Ngày Thuộc chủ đề:_Trắc nghiệm Hình học OXYZ Tag với:,

Câu hỏi: (Chuyên Lê Quý Đôn - Điện Biên - 2022) Trong không gian với hệ trục tọa độ \(Oxyz\), cho điểm \(A\left( {a;b;c} \right)\) với \(a;b;c\) là các số thực dương thỏa mãn \(5\left( {{a^2} + {b^2} + {c^2}} \right) = 9\left( {ab + 2bc + ca} \right)\) và \(Q = \frac{a}{{{b^2} + {c^2}}} - \frac{1}{{{{\left( {a + b + c} \right)}^3}}}\) có giá trị lớn nhất. Gọi \(M,N,P\) lần … [Đọc thêm...] về

(Chuyên Lê Quý Đôn – Điện Biên – 2022) Trong không gian với hệ trục tọa độ \(Oxyz\), cho điểm \(A\left( {a;b;c} \right)\) với \(a;b;c\) là các số thực dương thỏa mãn \(5\left( {{a^2} + {b^2} + {c^2}} \right) = 9\left( {ab + 2bc + ca} \right)\) và \(Q = \frac{a}{{{b^2} + {c^2}}} – \frac{1}{{{{\left( {a + b + c} \right)}^3}}}\) có giá trị lớn nhất. Gọi \(M,N,P\) lần lượt là hình chiếu vuông góc của \(A\) lên các tia \(Ox,Oy,Oz\). Phương trình mặt phẳng \(\left( {MNP} \right)\) là

(THPT Kim Liên – Hà Nội – 2022) Cắt hình trụ \(\left( T \right)\) có bán kính \(R\) bởi một mặt phẳng song song với trục và cách trục một khoảng bằng \(a\,\left( {0 < a < R} \right)\) ta được thiết diện là một hình vuông có diện tích \(16{a^2}\). Diện tích xung quanh của hình trụ \(\left( T \right)\) bằng

Ngày Thuộc chủ đề:Trắc nghiệm Khối tròn xoay Tag với:, ,

Câu hỏi: (THPT Kim Liên - Hà Nội - 2022) Cắt hình trụ \(\left( T \right)\) có bán kính \(R\) bởi một mặt phẳng song song với trục và cách trục một khoảng bằng \(a\,\left( {0 < a < R} \right)\) ta được thiết diện là một hình vuông có diện tích \(16{a^2}\). Diện tích xung quanh của hình trụ \(\left( T \right)\) bằng A. \(4\pi {a^2}\sqrt 5 \). B. \(\pi … [Đọc thêm...] về

(THPT Kim Liên – Hà Nội – 2022) Cắt hình trụ \(\left( T \right)\) có bán kính \(R\) bởi một mặt phẳng song song với trục và cách trục một khoảng bằng \(a\,\left( {0 < a < R} \right)\) ta được thiết diện là một hình vuông có diện tích \(16{a^2}\). Diện tích xung quanh của hình trụ \(\left( T \right)\) bằng

(Sở Ninh Bình 2022) Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành, có thể tích là \(V\). Gọi \(M\) là trung điểm của cạnh \(SA,N\) là điểm trên cạnh \(SB\) sao cho \(SN = 3NB\). Mặt phẳng \((P)\) thay đổi đi qua các điểm \(M,N\) và cắt các cạnh \(SC,SD\) lần lượt tại hai điểm phân biệt \(P,Q\). Tìm giá trị lớn nhất của thể tích khối chóp \(S.MNPQ\).

Ngày Thuộc chủ đề:Trắc nghiệm Thể tích đa diện Tag với:,

Câu hỏi: (Sở Ninh Bình 2022) Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành, có thể tích là \(V\). Gọi \(M\) là trung điểm của cạnh \(SA,N\) là điểm trên cạnh \(SB\) sao cho \(SN = 3NB\). Mặt phẳng \((P)\) thay đổi đi qua các điểm \(M,N\) và cắt các cạnh \(SC,SD\) lần lượt tại hai điểm phân biệt \(P,Q\). Tìm giá trị lớn nhất của thể tích khối chóp … [Đọc thêm...] về

(Sở Ninh Bình 2022) Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành, có thể tích là \(V\). Gọi \(M\) là trung điểm của cạnh \(SA,N\) là điểm trên cạnh \(SB\) sao cho \(SN = 3NB\). Mặt phẳng \((P)\) thay đổi đi qua các điểm \(M,N\) và cắt các cạnh \(SC,SD\) lần lượt tại hai điểm phân biệt \(P,Q\). Tìm giá trị lớn nhất của thể tích khối chóp \(S.MNPQ\).

(Sở Hà Tĩnh 2022) Cắt hình nón \(\left( N \right)\) bởi mặt phẳng đi qua đỉnh \(\left( S \right)\) và tạo bởi với trục của \(\left( N \right)\) một góc bằng \(30^\circ \) ta được thiết diện là tam giác \(SAB\) vuông và có diện tích \(4{a^2}\). Chiều cao của hình nón bằng:

Ngày Thuộc chủ đề:Trắc nghiệm Khối tròn xoay Tag với:, ,

Câu hỏi: (Sở Hà Tĩnh 2022) Cắt hình nón \(\left( N \right)\) bởi mặt phẳng đi qua đỉnh \(\left( S \right)\) và tạo bởi với trục của \(\left( N \right)\) một góc bằng \(30^\circ \) ta được thiết diện là tam giác \(SAB\) vuông và có diện tích \(4{a^2}\). Chiều cao của hình nón bằng: A. \(a\sqrt 3 \). B. \(2a\sqrt 3 \). C. \(2a\sqrt 2 \). D. \(a\sqrt 2 … [Đọc thêm...] về

(Sở Hà Tĩnh 2022) Cắt hình nón \(\left( N \right)\) bởi mặt phẳng đi qua đỉnh \(\left( S \right)\) và tạo bởi với trục của \(\left( N \right)\) một góc bằng \(30^\circ \) ta được thiết diện là tam giác \(SAB\) vuông và có diện tích \(4{a^2}\). Chiều cao của hình nón bằng:

(Sở Ninh Bình 2022) Cho hình chóp tứ giác đều \(S.ABCD\). Một mặt cầu \((J)\) ( \(J\) và \(S\) cùng phía với \((ABCD)\)) tiếp xúc với \((ABCD)\) tại \(A\), đồng thời tiếp xúc ngoài với mặt cầu nội tiếp hình chóp. Một mặt phẳng \((P)\) đi qua \(J\) và \(BC\). Gọi \(\varphi \) là góc giữa \((P)\) và \((ABCD)\). Tính \(\tan \varphi \) biết các đường chéo của thiết diện của hình chóp cắt bởi \((P)\) lần lượt cắt và vuông góc với \(SA,SD\).

Ngày Thuộc chủ đề:Trắc nghiệm Thể tích đa diện Tag với:,

Câu hỏi: (Sở Ninh Bình 2022) Cho hình chóp tứ giác đều \(S.ABCD\). Một mặt cầu \((J)\) ( \(J\) và \(S\) cùng phía với \((ABCD)\)) tiếp xúc với \((ABCD)\) tại \(A\), đồng thời tiếp xúc ngoài với mặt cầu nội tiếp hình chóp. Một mặt phẳng \((P)\) đi qua \(J\) và \(BC\). Gọi \(\varphi \) là góc giữa \((P)\) và \((ABCD)\). Tính \(\tan \varphi \) biết các đường chéo của thiết … [Đọc thêm...] về

(Sở Ninh Bình 2022) Cho hình chóp tứ giác đều \(S.ABCD\). Một mặt cầu \((J)\) ( \(J\) và \(S\) cùng phía với \((ABCD)\)) tiếp xúc với \((ABCD)\) tại \(A\), đồng thời tiếp xúc ngoài với mặt cầu nội tiếp hình chóp. Một mặt phẳng \((P)\) đi qua \(J\) và \(BC\). Gọi \(\varphi \) là góc giữa \((P)\) và \((ABCD)\). Tính \(\tan \varphi \) biết các đường chéo của thiết diện của hình chóp cắt bởi \((P)\) lần lượt cắt và vuông góc với \(SA,SD\).