Xét các số thực không âm \(x\), \(y\) thỏa mãn \({\log _5}{\left[ {\left( {x + 2} \right)\left( {y + 1} \right)} \right]^{y + 1}} = 125 - \left( {x - 1} \right)\left( {y + 1} \right)\). Khi biểu thức \(x + 5y\) đạt giá trị nhỏ nhất, giá trị của biểu thức \(5x + y\) bằng A. \(117\). B. \(118\). C. \(119\). D. \(120\). Lời giải: Ta có: \({\log _5}{\left[ {\left( … [Đọc thêm...] vềXét các số thực không âm \(x\), \(y\) thỏa mãn \({\log _5}{\left[ {\left( {x + 2} \right)\left( {y + 1} \right)} \right]^{y + 1}} = 125 – \left( {x – 1} \right)\left( {y + 1} \right)\). Khi biểu thức \(x + 5y\) đạt giá trị nhỏ nhất, giá trị của biểu thức \(5x + y\) bằng
Kết quả tìm kiếm cho: ty so
Cho \(x\) và \(y\) là các số thực không âm thỏa mãn \({\log _2}\left( {y + \sqrt {y + {2^x}} } \right) = 2x\). Khi biểu thức \(y – {2^{x + 2}}\) đạt giá trị nhỏ nhất, giá trị của biểu thức \(y + {2^x}\) bằng?
Cho \(x\) và \(y\) là các số thực không âm thỏa mãn \({\log _2}\left( {y + \sqrt {y + {2^x}} } \right) = 2x\). Khi biểu thức \(y - {2^{x + 2}}\) đạt giá trị nhỏ nhất, giá trị của biểu thức \(y + {2^x}\) bằng? A. \(\frac{5}{2}\). B. \(\frac{{25}}{4}\). C. \(\frac{{25}}{2}\). D. \(\frac{4}{{25}}\). Lời giải: Ta có: \(\begin{array}{l}{\log _2}\left( {y + \sqrt … [Đọc thêm...] vềCho \(x\) và \(y\) là các số thực không âm thỏa mãn \({\log _2}\left( {y + \sqrt {y + {2^x}} } \right) = 2x\). Khi biểu thức \(y – {2^{x + 2}}\) đạt giá trị nhỏ nhất, giá trị của biểu thức \(y + {2^x}\) bằng?
nbsp; Cho hàm số \(y = {m^2}{x^4} – 2\left( {m + 2024} \right){x^2} + 9\). Có bao nhiêu giá trị nguyên của \(m\) để hàm số đã cho nghịch biến trên khoảng \(\left( {1\,;2} \right)\) ?
nbsp; Cho hàm số \(y = {m^2}{x^4} - 2\left( {m + 2024} \right){x^2} + 9\). Có bao nhiêu giá trị nguyên của \(m\) để hàm số đã cho nghịch biến trên khoảng \(\left( {1\,;2} \right)\) ? A. \(46\). B. \(45\). C. \(44\). D. \(47\). Lời giải: +) TH1: \(m = 0\) Hàm số đã cho trở thành: \(y = - 4048{x^2} + 9\). Dễ thấy hàm … [Đọc thêm...] vềnbsp; Cho hàm số \(y = {m^2}{x^4} – 2\left( {m + 2024} \right){x^2} + 9\). Có bao nhiêu giá trị nguyên của \(m\) để hàm số đã cho nghịch biến trên khoảng \(\left( {1\,;2} \right)\) ?
Gọi \(S\) là tập hợp tất cả các giá trị thực của tham số \(m\) để đồ thị \(\left( C \right)\) của hàm số \(y = {x^4} – 2{m^2}{x^2} + {m^4} + 5\) có ba điểm cực trị, đồng thời ba điểm cực trị đó cùng với gốc tọa độ \(O\) tạo thành một tứ giác nội tiếp. Tìm tích các phần tử của \(S\).
Gọi \(S\) là tập hợp tất cả các giá trị thực của tham số \(m\) để đồ thị \(\left( C \right)\) của hàm số \(y = {x^4} - 2{m^2}{x^2} + {m^4} + 5\) có ba điểm cực trị, đồng thời ba điểm cực trị đó cùng với gốc tọa độ \(O\) tạo thành một tứ giác nội tiếp. Tìm tích các phần tử của \(S\). A. 2. B. \(\frac{1}{5}\). C. \( - \frac{1}{5}\). … [Đọc thêm...] vềGọi \(S\) là tập hợp tất cả các giá trị thực của tham số \(m\) để đồ thị \(\left( C \right)\) của hàm số \(y = {x^4} – 2{m^2}{x^2} + {m^4} + 5\) có ba điểm cực trị, đồng thời ba điểm cực trị đó cùng với gốc tọa độ \(O\) tạo thành một tứ giác nội tiếp. Tìm tích các phần tử của \(S\).
Cho hàm số \(y = \frac{{\ln x – 6}}{{\ln x – 3m}}\) với \(m\) là tham số. Gọi \(S\) là tập hợp các giá trị nguyên dương của \(m\) để hàm số đồng biến trên khoảng \(\left( {1;{\rm{e}}} \right)\). Tìm số phần tử của \(S\).
Cho hàm số \(y = \frac{{\ln x - 6}}{{\ln x - 3m}}\) với \(m\) là tham số. Gọi \(S\) là tập hợp các giá trị nguyên dương của \(m\) để hàm số đồng biến trên khoảng \(\left( {1;{\rm{e}}} \right)\). Tìm số phần tử của \(S\). A. \(2\). B.\(4\). C. \(3\). D. \(1\). Lời giải: Điều kiện \(\ln x - 3m \ne 0\)\( \Leftrightarrow m \ne … [Đọc thêm...] về Cho hàm số \(y = \frac{{\ln x – 6}}{{\ln x – 3m}}\) với \(m\) là tham số. Gọi \(S\) là tập hợp các giá trị nguyên dương của \(m\) để hàm số đồng biến trên khoảng \(\left( {1;{\rm{e}}} \right)\). Tìm số phần tử của \(S\).
Tìm tất cả các giá trị thực của \(m\) để hàm số \(y = \left( {m – {x^3}} \right)\sqrt {1 – {x^3}} \) đồng biến trên \(\left( {0;{\rm{ }}1} \right)\).
Tìm tất cả các giá trị thực của \(m\) để hàm số \(y = \left( {m - {x^3}} \right)\sqrt {1 - {x^3}} \) đồng biến trên \(\left( {0;{\rm{ }}1} \right)\). A. \(m < 1\). B. \(m \le - 2\). C. \(m > 1\). D. \(m \ge - 2\). Lời giải: + Tập xác định: \(D = \left( { - \infty ;{\rm{ 1}}} \right]\). + \(y' = - … [Đọc thêm...] vềTìm tất cả các giá trị thực của \(m\) để hàm số \(y = \left( {m – {x^3}} \right)\sqrt {1 – {x^3}} \) đồng biến trên \(\left( {0;{\rm{ }}1} \right)\).
Cho hàm số \(y = f\left( x \right)\)liên tục trên \(R\)và có bảng biến thiên như hình vẽ.
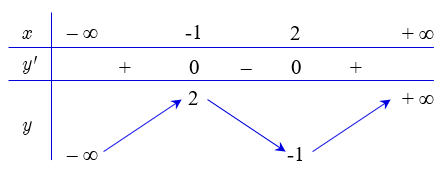
Xét hàm số \(g\left( x \right) = {e^{f\left( {2x + m} \right)}}\). Tìm số giá trị nguyên của tham số \(m \in \left[ { – 2024;2024} \right]\)để hàm số \(g\left( x \right)\)đồng biến trên \(\left( {1;3} \right)\).
Cho hàm số \(y = f\left( x \right)\)liên tục trên \(R\)và có bảng biến thiên như hình vẽ. Xét hàm số \(g\left( x \right) = {e^{f\left( {2x + m} \right)}}\). Tìm số giá trị nguyên của tham số \(m \in \left[ { - 2024;2024} \right]\)để hàm số \(g\left( x \right)\)đồng biến trên \(\left( {1;3} \right)\). A.\(4041\). B. \(2018\). C.\(2025\). … [Đọc thêm...] vềCho hàm số \(y = f\left( x \right)\)liên tục trên \(R\)và có bảng biến thiên như hình vẽ.
Xét hàm số \(g\left( x \right) = {e^{f\left( {2x + m} \right)}}\). Tìm số giá trị nguyên của tham số \(m \in \left[ { – 2024;2024} \right]\)để hàm số \(g\left( x \right)\)đồng biến trên \(\left( {1;3} \right)\).
Cho hàm số \(f\left( x \right) = {x^3} + a{x^2} + bx + c\) có đồ thị hàm số như hình dưới đây. Hàm số \(g\left( x \right) = f\left( {{x^2} + 3x + 1} \right)\) đồng biến trên khoảng nào?
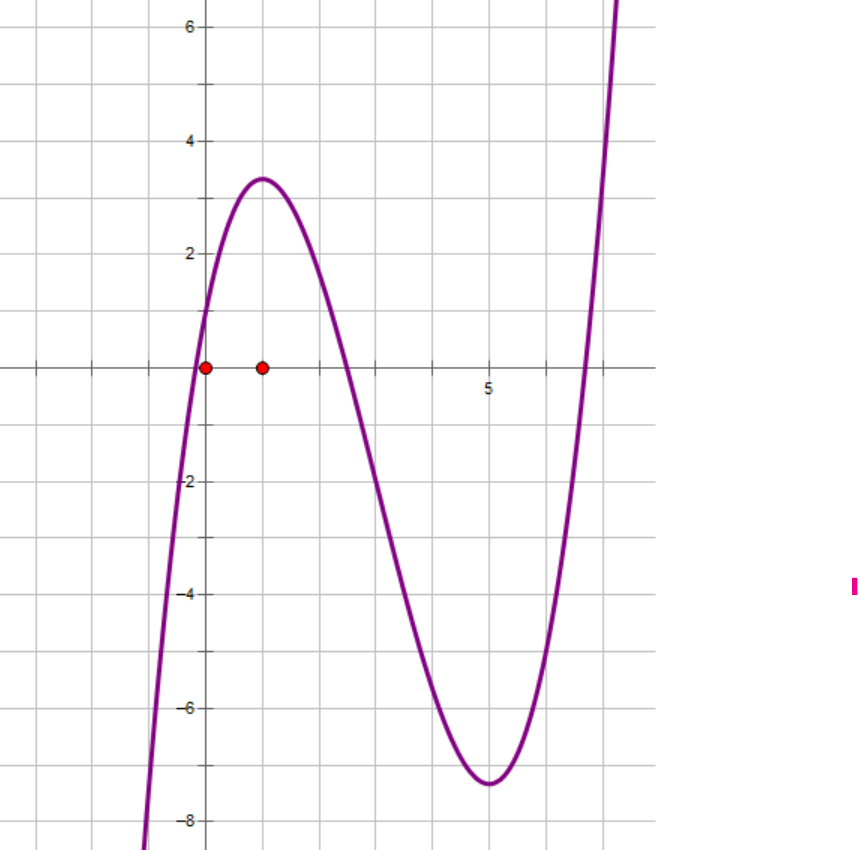
Cho hàm số \(f\left( x \right) = {x^3} + a{x^2} + bx + c\) có đồ thị hàm số như hình dưới đây. Hàm số \(g\left( x \right) = f\left( {{x^2} + 3x + 1} \right)\) đồng biến trên khoảng nào? A. \(\left( { - 4; - 3} \right)\). B. \(\left( { - 2;0} \right).\) C. \(\left( { - \frac{3}{2};1} \right)\) D. \(\left( { - 3; - 2} … [Đọc thêm...] về Cho hàm số \(f\left( x \right) = {x^3} + a{x^2} + bx + c\) có đồ thị hàm số như hình dưới đây. Hàm số \(g\left( x \right) = f\left( {{x^2} + 3x + 1} \right)\) đồng biến trên khoảng nào?
Đề ôn tập thi CK2 Toán 11 (mẫu 2025) – KNTT – 2024 – số 5 -.docx
Đề ôn tập thi CK2 Toán 11 (mẫu 2025) - KNTT - 2024 - số 5 -.docx ================ Để có thêm nguồn tư liệu phong phú trong quá trình ôn tập cho kì thi HK2 sắp tới, Booktoan.com chia sẻ đến các em Bộ đề thi thử HK2 môn Toán năm 2024 các trường cả nước. Đề có đáp án chi tiết giúp các em đối chiếu, tham khảo để đánh giá năng lực bản thân nhằm có kế hoạch ôn luyện tốt hơn. … [Đọc thêm...] vềĐề ôn tập thi CK2 Toán 11 (mẫu 2025) – KNTT – 2024 – số 5 -.docx
Đề ôn tập thi CK2 Toán 11 (mẫu 2025) – CTST – 2024 – số 1 FILE docx
Đề ôn tập thi CK2 Toán 11 (mẫu 2025) - CTST - 2024 - số 1 FILE docx ================ Để có thêm nguồn tư liệu phong phú trong quá trình ôn tập cho kì thi HK2 sắp tới, Booktoan.com chia sẻ đến các em Bộ đề thi thử HK2 môn Toán năm 2024 các trường cả nước. Đề có đáp án chi tiết giúp các em đối chiếu, tham khảo để đánh giá năng lực bản thân nhằm có kế hoạch ôn luyện tốt hơn. … [Đọc thêm...] vềĐề ôn tập thi CK2 Toán 11 (mẫu 2025) – CTST – 2024 – số 1 FILE docx
