Ông An có một tấm tôn có dạng nửa đường tròn bán kính $r=3$ m

Ông An có một tấm tôn có dạng nửa đường tròn bán kính $r=3$ m. Ông muốn cắt ra một hình chữ nhật nội tiếp nửa đường tròn đó để làm biển quảng cáo. Khi biển quảng cáo đó có diện tích lớn nhất thì chiều dài của tấm biển bằng bao nhiêu mét?.
Đáp án: 4,24

Lời giải:

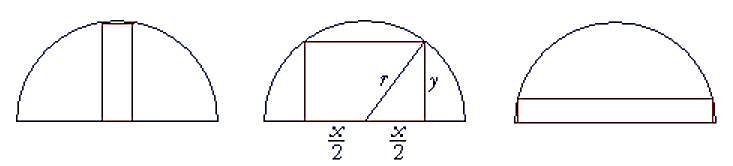
Ký hiệu các kích thước của hình chữ nhật như hình vẽ.
Ta có ${{\left( \dfrac{x}{2} \right)}^{2}}+{{y}^{2}}={{r}^{2}}$ $\Rightarrow {{y}^{2}}={{r}^{2}}-\dfrac{{{x}^{2}}}{4}=9-\dfrac{{{x}^{2}}}{4}$. ĐK: $0{<}x{
Diện tích của tấm biển hình chữ nhật là $S=xy$.
Ta có ${{S}^{2}}={{x}^{2}}{{y}^{2}}$ $={{x}^{2}}\left( 9-\dfrac{{{x}^{2}}}{4} \right)$ $=-\dfrac{1}{4}{{x}^{4}}+9{{x}^{2}}$ $=f\left( x \right)$.
${f}’\left( x \right)=-{{x}^{3}}+18x$; ${f}’\left( x \right)=0\Leftrightarrow x=3\sqrt{2}$.
BBT:

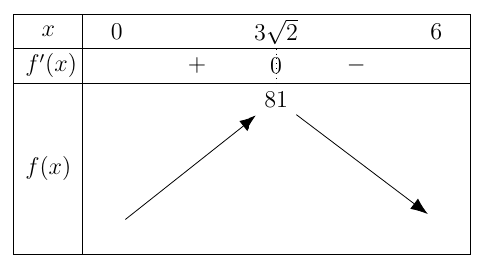
Suy ra ${{S}^{2}}\le 81$. Hay $\max S=9$, đạt được khi $x=3\sqrt{2}$ và $y=\dfrac{3}{\sqrt{2}}$.
Khi đó, chiều dài của hình chữ nhật là $x=3\sqrt{2}\approx 4,24$.