Nhìn vào bảng biến thiên dưới đây. Số nghiệm của phương trình $2f(x)+1=0$ là

Bài toán gốc

Nhìn vào bảng biến thiên dưới đây. Số nghiệm của phương trình $2f(x)+1=0$ là

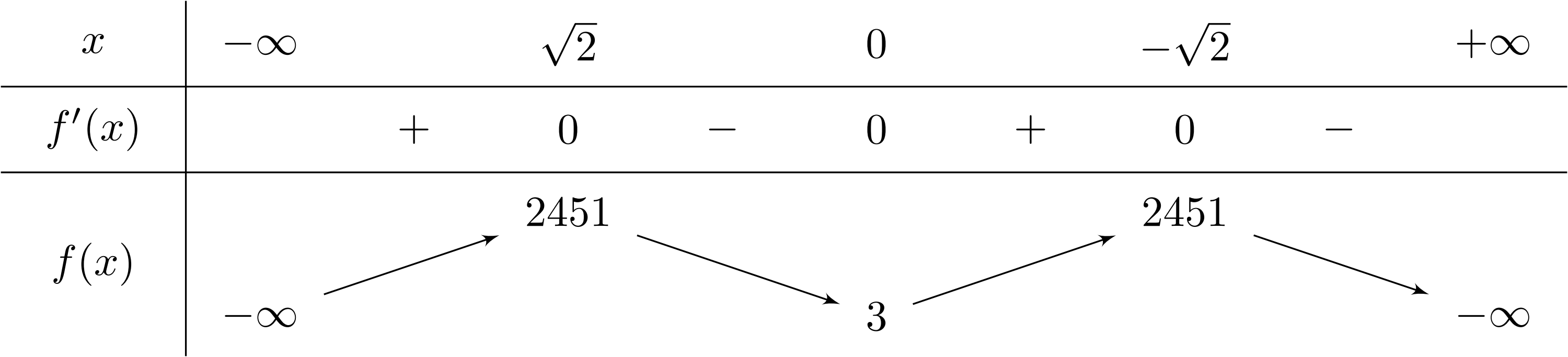
A. $3$.B. $2$.C. $1$.D. $0$.

Lời giải: Ta có phương trình $2f(x)+1=0 \Leftrightarrow f(x)=-\dfrac{1}{2}$.
Do đó số nghiệm phương trình bằng số giao điểm của đường thẳng $y=-\dfrac{1}{2}$ và đồ thị.
Dựa vào đồ thị hàm số trên, ta thấy đường thẳng $y=-\dfrac{1}{2}$ không cắt đồ thị nên phương trình $2f(x)+1=0$ vô nghiệm.

Phân tích và Phương pháp giải

Dạng bài toán yêu cầu tìm số nghiệm của phương trình $Af(x) + B = 0$ dựa vào Bảng biến thiên (BBT) của hàm số $f(x)$. Phương pháp giải là cô lập $f(x)$, đưa phương trình về dạng $f(x) = k$. Số nghiệm của phương trình chính là số giao điểm của đường thẳng nằm ngang $y = k$ và đồ thị hàm số $y = f(x)$, được xác định bằng cách so sánh giá trị $k$ với các giá trị cực trị của hàm số trên BBT.

Bài toán tương tự

Sau đây là 5 bài toán tương tự cùng dạng (sử dụng cấu trúc hàm số liên tục, bậc ba điển hình, có 2 cực trị $CĐ$ và $CT$).

**BBT chung cho 5 bài toán dưới đây:**
x | $-\infty$ | $-2$ | $2$ | $+\infty$
–|—|—|—|—
y’| $+$ | $0$ | $-$ | $0$ | $+
$y | $-\infty$ $\nearrow$ $4$ $\searrow$ $-2$ $\nearrow$ $+\infty$

**1. Số nghiệm bằng 3 (Đường thẳng $y=k$ cắt 3 điểm)**

**Câu 1.** Nhìn vào bảng biến thiên trên. Số nghiệm của phương trình $f(x) – 1 = 0$ là:

**A.** $4$. **B.** $3$. **C.** $2$. **D.** $1$.

Đáp án đúng: **B.**

Lời giải ngắn gọn: Ta có $f(x) = 1$. Dựa vào BBT, giá trị cực đại là $4$ và cực tiểu là $-2$. Vì $-2 < 1 < 4$, đường thẳng $y=1$ cắt đồ thị tại 3 điểm phân biệt. Số nghiệm là 3. **2. Số nghiệm bằng 2 (Đường thẳng $y=k$ tiếp xúc tại cực trị)** **Câu 2.** Nhìn vào bảng biến thiên trên. Số nghiệm của phương trình $2f(x) – 8 = 0$ là: **A.** $0$. **B.** $1$. **C.** $2$. **D.** $3$. Đáp án đúng: **C.** Lời giải ngắn gọn: Ta có $2f(x) – 8 = 0 \Leftrightarrow f(x) = 4$. Đường thẳng $y=4$ đi qua điểm cực đại (tiếp xúc) và cắt nhánh còn lại tại 1 điểm. Tổng cộng có 2 nghiệm phân biệt. **3. Số nghiệm bằng 1 (Đường thẳng $y=k$ nằm ngoài khoảng cực trị)** **Câu 3.** Nhìn vào bảng biến thiên trên. Số nghiệm của phương trình $f(x) + 3 = 0$ là: **A.** $4$. **B.** $3$. **C.** $2$. **D.** $1$. Đáp án đúng: **D.** Lời giải ngắn gọn: Ta có $f(x) = -3$. Vì $-3 < -2$ (giá trị cực tiểu), đường thẳng $y=-3$ chỉ cắt đồ thị tại 1 điểm duy nhất (nhánh đi từ $-\infty$ đến $x=-2$). **4. Số nghiệm bằng 0 (Phương trình vô nghiệm)** **Câu 4.** Nhìn vào bảng biến thiên trên. Số nghiệm của phương trình $f(x) = 5$ là: **A.** $0$. **B.** $1$. **C.** $2$. **D.** $3$. Đáp án đúng: **A.** Lời giải ngắn gọn: Ta có $f(x) = 5$. Vì $5 > 4$ (giá trị cực đại), đường thẳng $y=5$ nằm hoàn toàn phía trên đồ thị và không cắt đồ thị. Số nghiệm là 0.

**5. Bài toán kết hợp hệ số khác**

**Câu 5.** Nhìn vào bảng biến thiên trên. Số nghiệm của phương trình $4f(x) + 4 = 0$ là:

**A.** $3$. **B.** $2$. **C.** $1$. **D.** $0$.

Đáp án đúng: **C.**

Lời giải ngắn gọn: Ta có $4f(x) + 4 = 0 \Leftrightarrow f(x) = -1$. Vì $-2 < -1 < 4$, đường thẳng $y=-1$ cắt đồ thị tại 3 điểm phân biệt. Số nghiệm là 3.
*Tái bút*: Lỗi đánh máy trong đáp án đã chọn. $y=-1$ cắt 3 điểm. Đáp án phải là A. Chọn lại đáp án đúng: **A.**