Người ta muốn xây một chiếc bể chứa nước có hình dạng là một khối hộp chữ nhật không nắp có thể tích bằng $\dfrac{500}{3}$ m3

Người ta muốn xây một chiếc bể chứa nước có hình dạng là một khối hộp chữ nhật không nắp có thể tích bằng $\dfrac{500}{3}$ m3. Biết đáy bể là một hình chữ nhật có chiều dài gấp đôi chiều rộng và giá thuê thợ xây là $150.000$ đồng/m2. Tính chi phí thuê nhân công là ít nhất.
Đáp án: 22,5

Lời giải: Giả sử đáy bể có chiều rộng là $x$ $\left( x{>}0 \right)$ và chiều cao của chiếc bể là $h$ $\left( h{>}0 \right)$.
Suy ra chiều dài của đáy bể là $2x$.
Theo giả thiết ta có: $V=x.2x.h=\dfrac{500}{3}$ $\Rightarrow h=\dfrac{500}{3.2{{x}^{2}}}=\dfrac{250}{3{{x}^{2}}}$.
Phần diện tích cần xây: $S=S\left( x \right)=x.2x+2.x.\dfrac{250}{3{{x}^{2}}}+2.2x.\dfrac{250}{3{{x}^{2}}}=2{{x}^{2}}+\dfrac{500}{x}$.
Chi phí thuê nhân công là ít nhất khi $S\left( x \right)$ đạt giá trị nhỏ nhất.
Ta có ${S}’\left( x \right)=4x-\dfrac{500}{{{x}^{2}}}$.
${S}’\left( x \right)=0\Rightarrow 4x-\dfrac{500}{{{x}^{2}}}=0\Leftrightarrow \dfrac{4{{x}^{3}}-500}{x}=0\Rightarrow x=5$.
Bảng biến thiên:

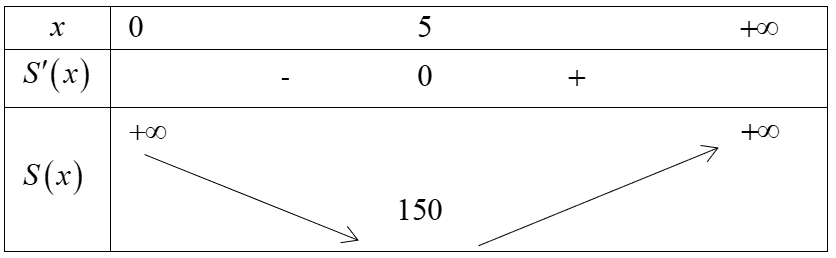
Phần diện tích $S$ cần xây đạt giá trị nhỏ nhất bằng $150$ m2.
Vậy chi phí thuê nhân công ít nhất là: $150.150000=22500000$ $=22,5$.