Người ta muốn làm một chiếc hộp kim loại hình hộp chữ nhật có thể tích $72\text{ c}{{\text{m}}^{3}}$ và đáy có chiều dài gấp đôi chiều rộng (Hình 3)

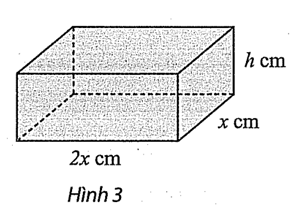
Người ta muốn làm một chiếc hộp kim loại hình hộp chữ nhật có thể tích $72\text{ c}{{\text{m}}^{3}}$ và đáy có chiều dài gấp đôi chiều rộng (Hình 3). Tính diện tích toàn phần nhỏ nhất đạt được của chiếc hộp (kết quả làm tròn đến hàng đơn vị của $\text{c}{{\text{m}}^{2}}$ ).

Đáp án: 108

Lời giải: Ta có $V=x.2x.h=72\Rightarrow h=\dfrac{36}{{{x}^{2}}}$.
Diện tích toàn phần của chiếc hộp là:
$S\left( x \right)=2\left( x.2x+xh+2xh \right)=2\left( 2{{x}^{2}}+3xh \right)=4{{x}^{2}}+\dfrac{216}{x},x{>}0$.
Ta có ${S}’\left( x \right)=8x-\dfrac{216}{{{x}^{2}}}$.
${S}’\left( x \right)=0\Leftrightarrow {{x}^{3}}=27\Leftrightarrow x=3$.
Bảng biến thiên:

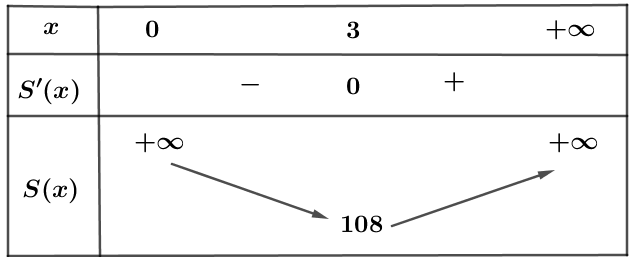
Vậy diện tích toàn phần nhỏ nhất của chiếc hộp là $108\text{ c}{{\text{m}}^{2}}$.