Người ta cần làm một hộp theo dạng một khối lăng trụ đều không nắp với thể tích lớn nhất từmột miếng tôn hình vuông có cạnh là 1 mét. Tính thể tích của hộp cần làm (làm tròn đến hàng phần trăm).
Đáp án: 0,07
Lời giải: Trả lời: $\dfrac{2}{27}$
Giả sử mỗi góc cắt đi một hình vuông x dm.
Khi đó chiều cao của hình hộp là $x\left( dm \right),\left( 0{<}x{
Và cạnh đáy của hộp là $\left( 1-2x \right)dm$.
Vậy thể tích của hộp là: $V=x{{\left( 1-2x \right)}^{2}}d{{m}^{3}}$
Ta có:
$V’=1-8x+12{{x}^{2}}$
Phương trình $V’=0\Leftrightarrow -8x+12{{x}^{2}}=0\Leftrightarrow x=\dfrac{1}{6}\in \left( 0;\dfrac{1}{2} \right)$
BBT
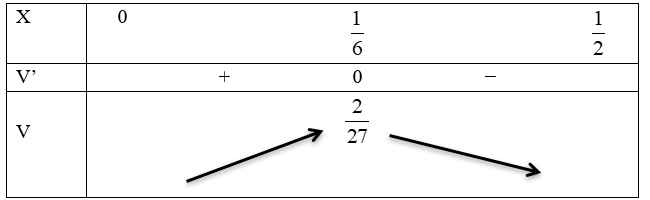
Vậy thể tích cần tìm là: $\dfrac{2}{27}d{{m}^{3}}$.
