Một nhà sản xuất muốn thiết kế một chiếc hộp có dạng hình hộp chữ nhật không có nắp có đáy hình vuông cạnh $x$ , đường cao $h$ và diện tích bề mặt bằng $S = 190\text{cm}^2$

Một nhà sản xuất muốn thiết kế một chiếc hộp có dạng hình hộp chữ nhật không có nắp có đáy hình vuông cạnh $x$ , đường cao $h$ và diện tích bề mặt bằng $S = 190\text{cm}^2$.
Tìm $x$ (làm tròn đến hàng phần mười) để thể tích của hộp là lớn nhất.
Đáp án: 8,0

Lời giải: Ta có diện tích bề mặt của hộp là $S = x^2 + 4xh$, với $x$ là cạnh đáy và $h$ là chiều cao.
Với $S = 190$, ta có $h = \dfrac{S – x^2}{4x}$.
Thể tích của hộp là $V = x^2h = x^2 \left(\dfrac{S – x^2}{4x}\right) = \dfrac{x(190 – x^2)}{4}$.
Ta có $V'(x) = \dfrac{95}{2} – \dfrac{3 x^{2}}{4}$; $V'(x) = 0$, ta được $x = \dfrac{\sqrt{570}}{3}, (x {>} 0)$.
Lập bảng biến thiên

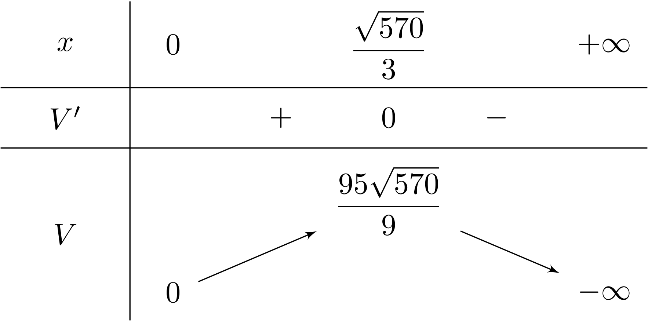
Thể tích lớn nhất của hộp là $V = \dfrac{95 \sqrt{570}}{9}$ tại $x = \dfrac{\sqrt{570}}{3} \approx 8{,}0$.endvabi