Một nhà sản xuất cần làm ra những chiếc bình có dạng hình trụ với dung tích $V = 860$ cm$^3$

Một nhà sản xuất cần làm ra những chiếc bình có dạng hình trụ với dung tích $V = 860$ cm$^3$. Mặt trên và mặt dưới của bình được làm bằng vật liệu có giá $1{,}4$ nghìn đồng/cm$^2$, trong khi mặt bên của bình được làm bằng vật liệu có giá $0{,}5$ nghìn đồng/cm$^2$. Tìm bán kính của bình để chi phí vật liệu sản xuất mỗi chiếc bình là nhỏ nhất.
Đáp án: 3,7

Lời giải: Gọi $r$ là bán kính đáy và $h$ là chiều cao của bình. Ta có:
\begin{align*}
V &= \pi r^2 h = 860 \Rightarrow h = \frac{860}{\pi r^2}
\end{align*}
Diện tích mặt trên và mặt dưới của bình là $2\pi r^2$. Diện tích mặt bên của bình là $2\pi rh$.
Chi phí để làm bình là:
\begin{align*}
C &= 1{,}4 \cdot 2\pi r^2 + 0{,}5 \cdot 2\pi rh
&= 2\cdot1{,}4\pi r^2 + 0{,}5 \cdot 2\pi r \left(\frac{860}{\pi r^2}\right)
&= 2\cdot1{,}4\pi r^2 + 0{,}5 \cdot \frac{2\cdot 860}{r}
\end{align*}
Đạo hàm của $C$ theo $r$ là
$C'(r) = 4\cdot1{,}4\pi r – \frac{0{,}5 \cdot 2 \cdot 860}{r^2}.$
Giải $C'(r) = 0$:
\begin{align*}
4\cdot1{,}4\pi r – \frac{2\cdot0{,}5 \cdot 860}{r^2} &= 0
4\cdot1{,}4\pi r^3 &= 2 \cdot 0{,}5 \cdot 860
r^3 &= \frac{2\cdot 0{,}5\cdot 860}{4\cdot1{,}4\cdot\pi}
r &\approx 3{,}7 \text{cm}
\end{align*}
Lập bảng biến thiên

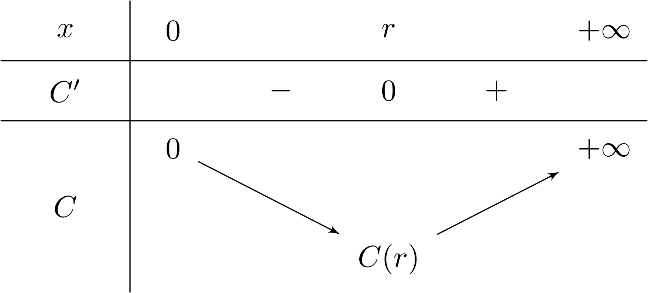
Vậy, bán kính đáy $r \approx 3{,}7 \text{cm}$ thì chi phí đạt giá trị nhỏ nhất.