Một nhà phân tích thị trường làm việc cho một công ty sản xuất thiết bị gia dụng nhận thấy rằng nếu công ty sản xuất và bán $x$ chiếc máy xay sinh tố hằng tháng thì lợi nhuận thu được (nghìn đồng) là $P(x)=-0,3 x^3+36 x^2+1800 x-48000

Một nhà phân tích thị trường làm việc cho một công ty sản xuất thiết bị gia dụng nhận thấy rằng nếu công ty sản xuất và bán $x$ chiếc máy xay sinh tố hằng tháng thì lợi nhuận thu được (nghìn đồng) là $P(x)=-0,3 x^3+36 x^2+1800 x-48000 .$ Lợi nhuận lớn nhất mà công ty có thể thu được khi sản xuất đúng bao nhiêu chiếc máy xay sinh tố mỗi tháng.
Đáp án: 100

Lời giải: Xét hàm số $y=P(x)=-0,3 x^3+36 x^2+1800 x-48000, x \geq 0$.
Ta có: ${y}’={P}'(x)=-0,9{{x}^{2}}+72x+1800;{y}’=0\Leftrightarrow x=100$
$\lim _{x \rightarrow+\infty} P(x)=-\infty$.
Bảng biến thiên:

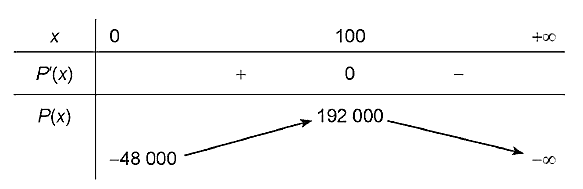
Do đó hàm số đồng biến trên nửa khoảng $[0 ; 100)$ và nghịch biến trên khoảng $(100 ;+\infty)$.
Tại $x=100$, hàm số đạt cực đại và ${{y}_{C}}=y(100)=192000$.
Vậy, lợi nhuận lớn nhất mà công ty có thể thu được là $y_{CÐ}=y(100)=192000$ (nghìn đồng), tức là 192 triệu đồng, đạt được khi sản xuất đúng 100 chiếc máy xay sinh tố mỗi tháng.