Một khu vui chơi giải trí giành cho trẻ em đang có kế hoạch điều chỉnh giá vé để tăng lợi nhuận. Sau khi khảo sát thị trường, người ta xác định được rằng: nếu giá vé vào cửa là 50000/người thì trung bình có 500 người đến. Nhưng nếu tăng thêm 1000/người thì sẽ mất 10 khách hàng hoặc giảm đi 1000/người thì sẽ có thêm 10 khách hàng trong số trung bình. Biết rằng, trung bình, mỗi khách hàng còn đem lại 5000 lợi nhuận trong các dịch vụ đi kèm. Hỏi giá vé vào cửa là bao nhiêu nghìn đồng để thu nhập là lớn nhất?
Lời giải
Đáp án: 47,5 (nghìn đồng).
Gọi giá vé vào cửa sau khi điều chỉnh là $50+x$ ( nghìn đồng); điều kiện: $50+x>0\Leftrightarrow x>-50$.
Số khách hàng đến sau khi điều chỉnh giá vé là $500-10x$ (người).
Khi đó tổng thu nhập là:
$\begin{align}
& f(x)=(50+x)(500-10x)+5.(500-10x) \\
& \begin{matrix}
{} & {} \\
\end{matrix}=-10{{x}^{2}}-50x+27500 \\
\end{align}$
Xét hàm số: $f(x)=-10{{x}^{2}}-50x+27500$
Bảng biến thiên:
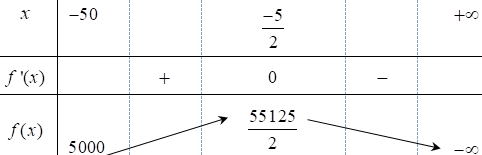
Dựa vào bảng biến thiên, ta có $f\left( x \right)$đạt giá trị lớn nhất tại $x=-\frac{5}{2}$.
Vậy để thu nhập lớn nhất thì giá vé vào cửa là $50-\frac{5}{2}=47,5$ (nghìn đồng).
Để lại một bình luận