Một hộp không nắp được làm từ một mảnh các tông theo hình vẽ

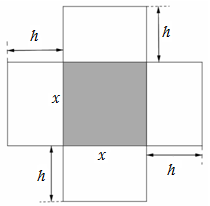
Một hộp không nắp được làm từ một mảnh các tông theo hình vẽ. Hộp có đáy là một hình vuông cạnh $x\left( \text{cm} \right)$, chiều cao là $h\left( \text{cm} \right)$ và thể tích là $4000\text{c}{{\text{m}}^{\text{3}}}.$ Tìm $x\left( \text{cm} \right)$ sao cho chiếc hộp làm ra tốn ít bìa các tông nhất.

Đáp án: 20

Lời giải: Thể tích hộp là: $V={{x}^{2}}h\Rightarrow h=\dfrac{V}{{{x}^{2}}}=\dfrac{4000}{{{x}^{2}}}$.
Diện tích các mặt của hộp (tổng diện tích bìa các tông để làm hộp) là:
$S=4xh+{{x}^{2}}\Rightarrow S=4x.\dfrac{4000}{{{x}^{2}}}+{{x}^{2}}=\dfrac{16000}{x}+{{x}^{2}}$ $\left( x{>}0 \right)$.
${S}’=-\dfrac{16000}{{{x}^{2}}}+2x$
${S}’=0\Leftrightarrow -\dfrac{16000}{{{x}^{2}}}+2x=0\Leftrightarrow 2{{x}^{3}}-16000=0\Leftrightarrow x=20$.
Bảng biến thiên $S$ :

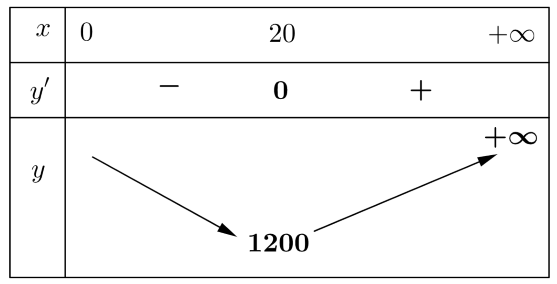
Vậy khi $x=20$ thì $S$ đạt giá trị nhỏ nhất là $1200c{{m}^{2}}$.
Cách 2: Sử dụng bất đẳng thức Caucy:
$S=\dfrac{16000}{x}+{{x}^{2}}=\dfrac{8000}{x}+\dfrac{8000}{x}+{{x}^{2}}\ge 3\sqrt[3]{\dfrac{8000}{x}.\dfrac{8000}{x}.{{x}^{2}}}=1200$.
Dấu “=” xảy ra khi và chỉ khi $\dfrac{8000}{x}={{x}^{2}}\Leftrightarrow x=20$.