Một hồ nước nhân tạo được xây dựng trong một công viên giải trí

Một hồ nước nhân tạo được xây dựng trong một công viên giải trí. Trong mô hình minh họa như hình vẽ, nó được giới hạn bởi các trục tọa độ và đồ thị của hàm số $y=f\left( x \right)=\dfrac{1}{10}\left( -{{x}^{3}}+9{{x}^{2}}-15x+56 \right)$. Đơn vị đo độ dài trên mỗi trục tọa độ là

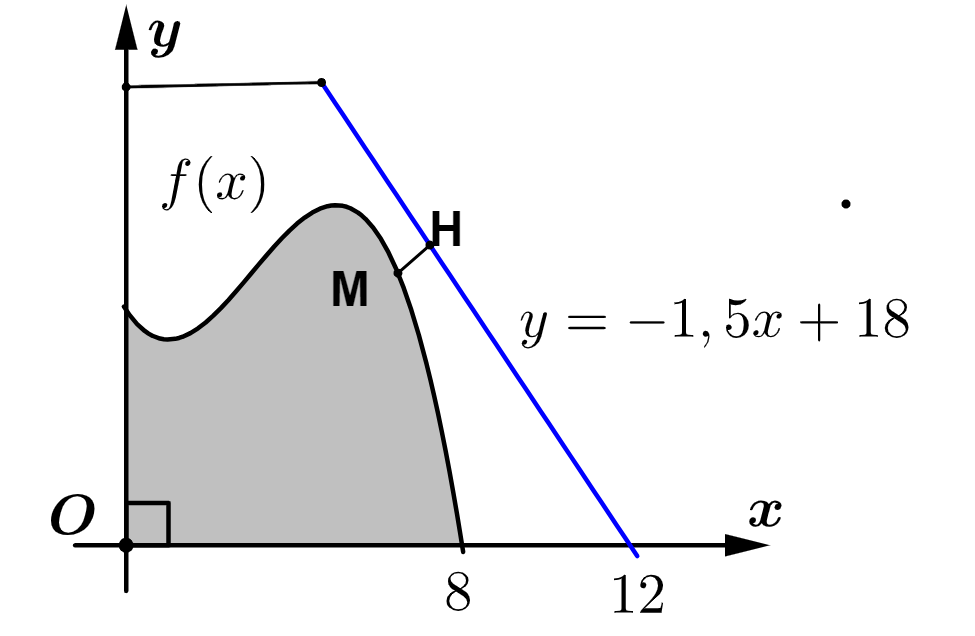
Trong công viên có một con đường chạy dọc theo đồ thị hàm số $y=-1,5x+18$. Người ta dự định xây dựng bên bờ hồ một bến thuyền đạp nước sao cho khoảng cách từ bến thuyền đến con đường này là ngắn nhất. Tọa độ của điểm để xây bến thuyền $M\left( {{x}_{0}};{{y}_{0}} \right)$.Tìm ${{x}_{0}}.$
Đáp án: 6

Lời giải: Ta có: $d\left( M;(d) \right)=\dfrac{\left| 1,5{{x}_{0}}+{{y}_{0}}-18 \right|}{\sqrt{{{1.5}^{2}}+1}}=\dfrac{\left| 1,5{{x}_{0}}+\dfrac{1}{10}\left( -{{x}_{0}}^{3}+9{{x}_{o}}^{2}-15{{x}_{o}}+56 \right)-18 \right|}{\dfrac{\sqrt{13}}{2}}$
$=\dfrac{\left| 15{{x}_{0}}+\left( -{{x}_{0}}^{3}+9{{x}_{o}}^{2}-15{{x}_{o}}+56 \right)-180 \right|}{5\sqrt{13}}=\dfrac{\left| -{{x}_{0}}^{3}+9{{x}_{o}}^{2}-124 \right|}{5\sqrt{13}}$
Xét hàm số: $h(x)=-{{x}^{3}}+9{{x}^{2}}-124$ trên $[0;8]$ ta có: $h'(x)=-3{{x}^{2}}+18x$;
Xét $h'(x)=0\Leftrightarrow -3{{x}^{2}}+18x=0\Leftrightarrow x=0;x=6$; Ta có: $h(0)=-124;h(6)=-16$ $h\left( 8 \right)=-60$
Vậy GTNN của: $d\left( M;(d) \right)=\dfrac{16}{5\sqrt{13}}$ khi ${{x}_{o}}=6$