Một đường dây điện được nối từ nhà máy thuỷ điện Hoà Bình trên đất liền ở vị trí $H$ đến đảo Dừa ở vị trí $D$ theo đường gấp khúc $HSD$ ( $S$ là một vị trí trên đất liền) như hình vẽ

Một đường dây điện được nối từ nhà máy thuỷ điện Hoà Bình trên đất liền ở vị trí $H$ đến đảo Dừa ở vị trí $D$ theo đường gấp khúc $HSD$ ( $S$ là một vị trí trên đất liền) như hình vẽ. Biết khoảng cách từ đảo Dừa vào đất liền là $DA=15km$ và khoảng cách $AH=40km$. Để lắp đặt đường dây điện đặt dưới nước có chi phí $6000USD/1km$, dây điện đặt trên đất liền có chi phí $3000USD/1km$.

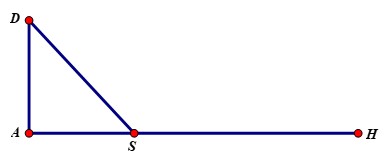
Để khi mắc dây điện từ $H$ qua $S$ rồi đến $D$ là ít tốn kém nhất thì điểm $S$ cách $A$ một đoạn là $a\sqrt{b}$. Tính $a+b$.
Đáp án: 8

Lời giải: Đặt $SA=x\left( km \right)$, với $0\le x\le 40$
Khi đó ta có : $DS=\sqrt{D{{A}^{2}}+A{{S}^{2}}}=\sqrt{225+{{x}^{2}}}$ $\left( km \right)$
Và $SH=AH-AS=40-x$ $\left( km \right)$.
Tổng chi phí lắp đặt đường điện $HSD$ là $T=6000.\sqrt{225+{{x}^{2}}}+3000.\left( 40-x \right)\left( USD \right)$.
Xét hàm số $f\left( x \right)=6\sqrt{225+{{x}^{2}}}+3\left( 40-x \right)$ với $0\le x\le 40$.
Có ${f}’\left( x \right)=\dfrac{6x}{\sqrt{225+{{x}^{2}}}}-3$.
Xét: ${f}’\left( x \right)=0\Leftrightarrow \dfrac{6x}{\sqrt{225+{{x}^{2}}}}-3=0\Leftrightarrow \left\{ \begin{array}{l} x\ge 0 \\ 4{{x}^{2}}=225+{{x}^{2}} \end{array} \right.\Leftrightarrow x=5\sqrt{3}\in \left[ 0;40 \right]$.
Ta có : $f\left( 0 \right)=210$,
$f\left( 5\sqrt{3} \right)=60\sqrt{3}+120-15\sqrt{3}=120+45\sqrt{3}$
$f\left( 40 \right)=30\sqrt{73}$
Suy ra: $\max\limits_{\left[ 0;40 \right]}f\left( x \right)=f\left( 5\sqrt{3} \right)$.
Do đó: chi phí ít nhất khi xây dựng đường điện $HSD$ là $120000+45000\sqrt{3}\approx 197942USD$
Đạt được khi $x=5\sqrt{3}\left( km \right)$
Suy ra: $\left\{ \begin{array}{l} a=5 \\ b=3 \end{array} \right.$
Vậy $a+b=8$