Một doanh nghiệp dự định sản xuất không quá 500 sản phẩm

Một doanh nghiệp dự định sản xuất không quá 500 sản phẩm. Nếu doanh nghiệp sản xuất $x$ sản phẩm ( $1\le x\le 500$ ) thì doanh thu nhận được khi bán hết số sản phẩm đó là $F\left( x \right)=x^3-1273x^2+226249x+22000$ (đồng), trong khi chi phí sản xuất bình quân cho một sản phẩm là $G\left( x \right)=x+800+\dfrac{23000}{x}$ (đồng). Doanh nghiệp cần sản xuất bao nhiêu sản phẩm để lợi nhuận thu được là lớn nhất?
Đáp án: 100

Lời giải: Lợi nhuận của doanh nghiệp khi sản xuất $x$ sản phẩm là: $L\left( x \right)=F\left( x \right)-xG\left( x \right)=x^3-1274x^2+225449x-1000$.
${L}’\left( x \right)=3x^2-2548x+225449$
${L}’\left( x \right)=3x^2-2548x+225449=0\Leftrightarrow \left[ \begin{array}{l} x=749 \\ x=\dfrac{301}{3} \end{array} \right.$,
$x=749\notin \left[ 0;500 \right]$, loại
Lập BBT của hàm số $f\left( x \right)$ trên đoạn $\left[ 0;500 \right]$ với $m=\dfrac{301}{3}$.

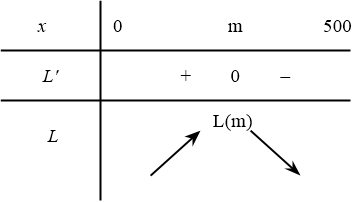
Do số sản phẩm là số nguyên, nên ta xét giá trị của hàm số tại hai điểm nguyên trước và sau giá trị $\dfrac{301}{3}$ là 100 và 101.
Ta có $L\left( 100 \right)=10803900;L\left( 101 \right)=10803576\Rightarrow L\left( 100 \right){>}L\left( 101 \right)$.
Do đó, doanh nghiệp nên sản xuất 100 sản phẩm để lợi nhuận thu được là lớn nhất.