Một cửa hàng trung bình bán được 100 cái Tivi mỗi tháng với giá 14 triệu đồng một cái. Chủ cửa hàng nhận thấy rằng, nếu giảm giá bán mỗi cái 500 ngàn đồng thì số lượng tivi bán ra sẽ tăng thêm 10 cái mỗi tháng. Hỏi cửa hàng nên bán với giá bao nhiêu để doanh thu cửa hàng là lớn nhất?
Đáp án: 9,5
Lời giải: Giả sử cần giảm giá bán mỗi cái tivi là $x$ triệu đồng $\left( x{
Do giảm giá bán mỗi cái 500 ngàn đồng thì số lượng tivi bán ra sẽ tăng thêm 10 cái mỗi tháng nên số lượng tivi bán ra tăng lên bây giờ là: $\dfrac{10x}{0,5}=20x$.
Khi đó, doanh thu một tháng của cửa hàng là $\left( 100+20x \right).\left( 14-x \right)=-20{{x}^{2}}+180x+1400$.
Xét hàm số $f\left( x \right)=-20{{x}^{2}}+180x+1400\left( x{
Ta có ${f}’\left( x \right)=-40x+180$; ${f}’\left( x \right)=0\Leftrightarrow x=4,5$.
Bảng biến thiên
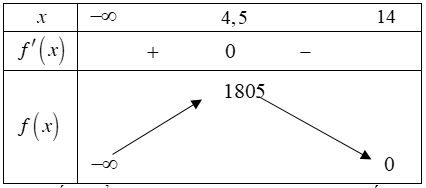
Từ bảng biến thiên ta thấy: Để doanh thu cửa hàng đạt cao nhất thì giá bán mỗi cái tivi là $14-4,5=9,5$ triệu đồng
Để lại một bình luận