Một công ty sản xuất đồ gia dụng ước tính chi phí để sản xuất $x$ (sản phẩm) là $C\left( x \right)=150x+900$ (nghìn đồng). Khi sản xuất càng nhiều sản phẩm thì chi phí sản xuất trung bình cho mỗi sản phẩm không vượt quá $t$ (nghìn đồng). Tìm giá trị nhỏ nhất của $t$.
Đáp án: 150
Lời giải: Chi phí sản xuất trung bình cho mỗi sản phẩm là $f\left( x \right)=\dfrac{C\left( x \right)}{x}=\dfrac{150x+900}{x}$.
Ta có ${f}’\left( x \right)=\dfrac{-900}{{{x}^{2}}}{}0$.
$\lim\limits_{x\to +\infty }f\left( x \right)=\lim\limits_{x\to +\infty }\dfrac{150x+900}{x}=150$.
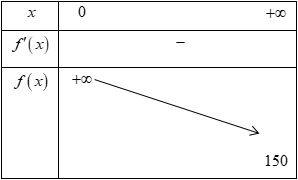
Vậy khi sản xuất càng nhiều sản phẩm thì chi phí sản xuất trung bình cho mỗi sản phẩm càng giảm, nhưng không dưới $150$ nghìn đồng.
Để lại một bình luận