Một công ty bất động sản có $50$ căn hộ cho thuê

Một công ty bất động sản có $50$ căn hộ cho thuê. Biết rằng nếu cho thuê mỗi căn hộ với giá $2.000.000$ đồng mỗi tháng thì mọi căn hộ đều có người thuê và cứ mỗi lần tăng giá cho thuê mỗi căn hộ $100.000$ đồng mỗi tháng thì có thêm 2 căn hộ bị bỏ trống. Muốn có lợi nhuận cao nhất, công ty đó phải cho thuê với giá mỗi căn hộ là bao nhiêu (đơn vị tính bằng triệu đồng và làm tròn kết quả tới hàng phần trăm)?
Đáp án: 2,25

Lời giải: Gọi $x$ là giá thuê thực tế của mỗi căn hộ, ( $x$ : đồng; $x\ge 2000000$ đồng)
Khi tăng giá 100.000 đồng thì có 2 căn hộ bị bỏ trống.
Tăng giá $x-2.000.000$ đồng, ta có số căn hộ bị bỏ trống là $\dfrac{2\left( x-2.000.000 \right)}{100.000}=\dfrac{x-2.000.000}{50.000}$
Khi cho thuê với giá $x$ đồng thì số căn hộ cho thuê là: $50-\dfrac{x-2.000.000}{50.000}=-\dfrac{x}{50.000}+90$
Gọi $F\left( x \right)$ là hàm lợi nhuận thu được khi cho thuê các căn hộ, ( $F\left( x \right)$ : đồng).
Ta có: $F\left( x \right)=\left( -\dfrac{x}{50.000}+90 \right)x=-\dfrac{1}{50.000}{{x}^{2}}+90x$
Ta tìm GTLN của $F\left( x \right)=-\dfrac{1}{50.000}{{x}^{2}}+90x$, $x\ge 2.000.000$
${F}’\left( x \right)=-\dfrac{1}{25.000}x+90$
${F}’\left( x \right)=0\Leftrightarrow -\dfrac{1}{25.000}x+90=0\Leftrightarrow x=2.250.000$
Bảng biến thiên:

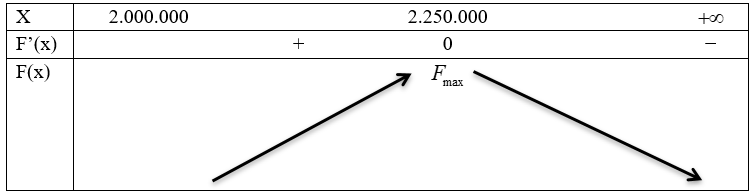
Suy ra $F\left( x \right)$ đạt giá trị lớn nhất khi $x=2.250.000$
Vậy công ty phải cho thuê với giá $2,25$ triệu đồng mỗi căn hộ thì thu được lợi nhuận lớn nhất.